
【题目】如图,等腰梯形ABCD中,AD∥BC,∠B=45°,P是BC边上一点,△PAD的面积为 ![]() ,设AB=x,AD=y
,设AB=x,AD=y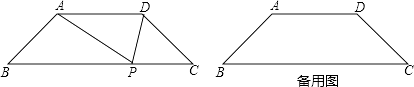
(1)求y与x的函数关系式;
(2)若∠APD=45°,当y=1时,求PBPC的值;
(3)若∠APD=90°,求y的最小值.
【答案】
(1)
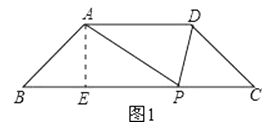
解:如图1,过A作AE⊥BC于点E,
在Rt△ABE中,∠B=45°,AB=x,
∴AE=ABsinB= ![]() x,
x,
∵S△APD= ![]() ADAE=
ADAE= ![]() ,
,
∴ ![]() y
y ![]() x=
x= ![]() ,
,
则y= ![]()
(2)
解:∵∠APC=∠APD+∠CPD=∠B+∠BAP,∠APD=∠B=45°,
∴∠BAP=∠CPD,
∵四边形ABCD为等腰梯形,
∴∠B=∠C,
∴△ABP∽△PCD,
∴ ![]() =
= ![]() ,
,
∴PBPC=ABDC=AB2,
当y=1时,x= ![]() ,即AB=
,即AB= ![]() ,
,
则PBPC=( ![]() )2=2
)2=2
(3)
解:如图2,取AD的中点F,连接PF,
过P作PH⊥AD,可得PF≥PH,
当PF=PH时,PF有最小值,
又∵∠APD=90°,
∴PF= ![]() AD=
AD= ![]() y,
y,
∴PH= ![]() y,
y,
∵S△APD= ![]() ADPH=
ADPH= ![]() ,
,
∴ ![]() y
y ![]() y≥
y≥ ![]() ,即y2≥2,
,即y2≥2,
∵y>0,
∴当取“=“时,y取最小值 ![]() ,
,
则y的最小值为 ![]()

【解析】(1)如图1,过A作AE垂直于BC,在直角三角形ABE中,由∠B=45°,AB=x,利用锐角三角函数定义表示出AE,三角形PAD的面积以AD为底,AE为高,利用三角形面积公式表示出,根据已知的面积即可列出y与x的函数关系式;(2)根据∠APC=∠APD+∠CPD,以及∠APC为三角形ABP的外角,利用外角性质得到关系式,等量代换得到∠BAP=∠CPD,再由四边形ABCD为等腰梯形,得到一对底角相等及AB=CD,可得出三角形ABP与三角形PDC相似,由相似得比例,将CD换为AB,由y的值求出x的值,即为AB的值,即可求出PBPC的值;(3)取AD的中点F,过P作PH垂直于AD,由直角三角形PF大于等于PH,当PF=PH时,PF最小,此时F与H重合,由三角形APD为直角三角形,利用直角三角形斜边上的中线等于斜边的一半得到PF等于AD的一半,表示出PF即为PH,三角形APD面积以AD为底,PH为高,利用三角形面积公式表示出三角形APD面积,由已知的面积求出y的值,即为最小值.
【考点精析】解答此题的关键在于理解三角形的外角的相关知识,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对等腰梯形的性质的理解,了解等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() ,
, ![]() ,点P为双曲线
,点P为双曲线 ![]() 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 ![]() 于D、C两点,则△PCD的面积为 .
于D、C两点,则△PCD的面积为 . 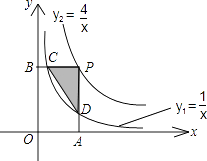
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=70°,∠C=40°,过点D作DE∥AB交BC于点E,若AD=3,BC=10,则CD的长是________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() (x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.

(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是___个单位长度;△AOC与△BOD关于直线对称,则对称轴是___;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是___度;
(2)连结AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() +1)米
+1)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距50千米.星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发 小时时,行进中的两车相距8千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】德国科学家贝塞尔推算出天鹅座第![]() 颗暗星距地球
颗暗星距地球![]() ,比太阳到地球的距离还远
,比太阳到地球的距离还远![]() 倍.
倍.
![]() 用科学记数法表示出暗星到地球的距离;
用科学记数法表示出暗星到地球的距离;
![]() 用科学记数法表示出
用科学记数法表示出![]() 这个数;
这个数;
![]() 如果光的速度大约是
如果光的速度大约是![]() ,那么你能计算出从暗星发出的光线到地球需要多少秒吗?用科学记数法表示出来.
,那么你能计算出从暗星发出的光线到地球需要多少秒吗?用科学记数法表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)在图1中,求证:![]() .
.
(2)在图1中,若点![]() 在
在![]() 上且
上且![]() ,试猜想
,试猜想![]() 、
、![]() 、
、![]() 之间的数量关系并证明.
之间的数量关系并证明.
(3)运用(1)(2)解答中所积累的经验知识,完成下题:如图2,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 上,
上,![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com