
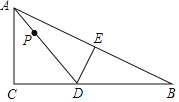
【题目】如图,Rt△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,点E在边AB上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P是线段AD上一动点,当半径为5的⊙P与△ABC的一边相切时,AP的长为_____.
【答案】![]() 或
或![]()
【解析】
设BD=x,由折叠性质得AD与CD,在Rt△ACD中由勾股定理列出x的方程,进而求得DE,得出⊙P不能与AB相切,进而分两种情况:⊙P与AC相切和⊙P与BC相切,过P作切线的垂线段,再根据相似三角形的比例线段便可求得结果.
解:设BD=x,由折叠知AD=BD=x,CD=16﹣x,
在Rt△ACD中,由勾股定理得,x2=82+(16﹣x)2,
解得,x=10,
∴CD=10,
∵AB=![]() =
=![]() =
=![]() ,
,
∴AE=BE=![]() AB=
AB=![]() ,
,
∴DE=![]() ,
,
∴点P是线段AD上运动时,⊙P不可能与AB相切,
分两种情况:①当⊙P与AC相切时,过点P作PF⊥AC于点F,如图1,
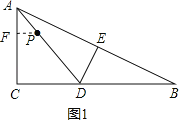
∴PF=5,PF∥CD,
∴△APF∽△ADC,
∴![]() ,即
,即![]() ,
,
∴![]() ;
;
②⊙P与BC相切时,过点P作PG⊥BC于点G,如图2,
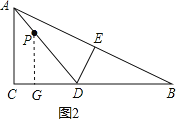
∴PG=5,PG∥AC,
∴△DPG∽△DAC,
∴![]() ,即
,即![]() ,
,
∴DP=![]() ,
,
∴AP=10﹣![]() =
=![]() ,
,
综上,AP的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】2020年3月“停课不停学”期间,某校采用简单随机抽样的方式调查本校学生参加第一天线上学习的时长,将收集到的数据制成不完整的频数分布表和扇形图,如下所示:
组别 | 学习时长(分钟) | 频数(人) |
第1组 | x≤40 | 3 |
第2组 | 40<x≤60 | 6 |
第3组 | 60<x≤80 | m |
第4组 | 80<x≤100 | 18 |
第5组 | 100<x≤120 | 14 |

(1)求m,n的值;
(2)学校有学生2400人,学校决定安排老师给““线上学习时长”在x≤60分钟范围内的学生打电话了解情况,请你根据样本估计学校学生“线上学习时长”在x≤60分钟范围内的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:
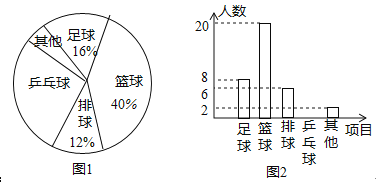
请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
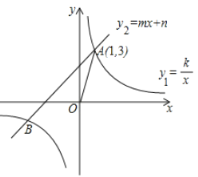
【题目】如图,反比例函数![]() 和一次函数
和一次函数![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求一次函数和反比例函数解析式;
(2)连接OA,试问在x轴上是否存在点P,使得![]() 为以OA为腰的等腰三角形,若存在,直接写出满足题意的点P的坐标;若不存在,说明理由.
为以OA为腰的等腰三角形,若存在,直接写出满足题意的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
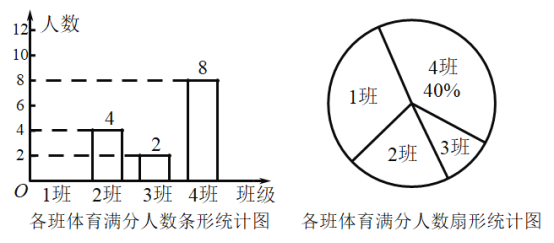
【题目】学校对八年级![]() 班的体育成绩做了模拟测评,将各个班的满分人数绘制成两幅不完整的统计图(如图):
班的体育成绩做了模拟测评,将各个班的满分人数绘制成两幅不完整的统计图(如图):
根据图中信息解答以下问题:
(1)扇形统计图中,“![]() 班”所在扇形的圆心角是 度,并补全条形统计图;
班”所在扇形的圆心角是 度,并补全条形统计图;
(2)班满分同学中有![]() 名(其中
名(其中![]() 女
女![]() 男)的跳远动作十分标准,
男)的跳远动作十分标准,![]() 班班主任准备从这名同学中任选
班班主任准备从这名同学中任选![]() 名给本班同学示范,请利用画树状图或列表的方法求出选出名同学恰好是一男一女的概率.
名给本班同学示范,请利用画树状图或列表的方法求出选出名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
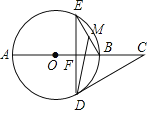
【题目】如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F,交⊙O于点E,点M是BE的中点,AB=4,∠E=∠C=30°.
(1)求证:CD是⊙O的切线;
(2)求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地推进太原市生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役的全面打响.某小区准备购买![]() 两种型号的垃圾箱,通过市场调研得知:购买3个
两种型号的垃圾箱,通过市场调研得知:购买3个![]() 型垃圾箱和2个
型垃圾箱和2个![]() 型垃圾箱共需540元,购买2个
型垃圾箱共需540元,购买2个![]() 型垃圾箱比购买3个
型垃圾箱比购买3个![]() 型垃圾箱少用160元.
型垃圾箱少用160元.

(1)求每个![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱各多少元?
型垃圾箱各多少元?
(2)该小区物业计划用不多于2100元的资金购买![]() 两种型号的垃圾箱共20个,则该小区最多可以购买
两种型号的垃圾箱共20个,则该小区最多可以购买![]() 型垃圾箱多少个.
型垃圾箱多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
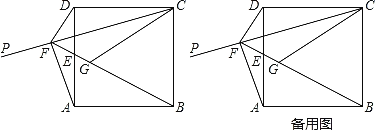
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com