
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
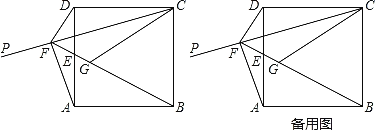
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
【答案】(1)DF⊥BF,见解析;(2)![]() ;(3)2﹣
;(3)2﹣![]()
【解析】
(1)由轴对称的性质可得CD=CG,DF=FG,由“SSS”可证△CDF≌△CGF,可得∠CDF=∠CGF,由等腰三角形的性质和四边形内角和定理可求∠DFB=90°,可得结论;
(2)过点C作CH⊥BF于H,由等腰直角三角形的性质可求CH=FH=4,由勾股定理可求CG=BC=CD=2![]() ,通过证明△AEB∽△HBC,可得
,通过证明△AEB∽△HBC,可得![]() ,即可求解;
,即可求解;
(3)连接BD,过点F作FM⊥AD于M,作∠AFN=∠FAD,交AD于N,由题意可证点D、F、A、B四点共圆,可得∠DBF=∠DAF,∠FDA=∠FBA,可求∠FDA=30°,∠FAD=15°,利用锐角三角函数即可求解.
解:(1)DF⊥BF,
理由如下:
∵点D关于射线CP的对称点G,
∴CD=CG,DF=FG,
又∵CF=CF,
∴△CDF≌△CGF(SSS),
∴∠CDF=∠CGF,
∵CD=CB=CG,
∴∠CGB=∠CBG,
∵∠CGB+∠CGF=180°,
∴∠CBG+∠CDF=180°,
∵∠CDF+∠DFB+∠CBF+∠DCB=360°,
∴180°+90°+∠DFB=360°,
∴∠DFB=90°,
∴DF⊥BF;
(2)如图,过点C作CH⊥BF于H,
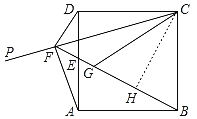
∵△CDF≌△CGF,∠DFB=90°,
∴∠CFD=∠CFG=45°,DF=FG=2,
∵CH⊥BF,
∴∠CFH=∠FCH=45°,
∴CH=FH,
∴CF=![]() CH=4
CH=4![]() ,
,
∴CH=FH=4,
∴GH=FH﹣FG=2,
∴CG![]() ,
,
∴CD=CG=BC=AB=![]() ,
,
∵CB=CG,CH⊥BG,
∴BH=GH=2,
∵AD∥BC,
∴∠AEB=∠CBH,
又∵∠DAB=∠CHB=90°,
∴△AEB∽△HBC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ;
;
(3)连接BD,过点F作FM⊥AD于M,作∠AFN=∠FAD,交AD于N,

∵四边形ABCD是正方形,
∴∠ABD=∠ADB=45°,
∵∠DFB=∠DAB=90°,
∴点D、F、A、B四点共圆,
∴∠DBF=∠DAF,∠FDA=∠FBA,
∵∠ABD=∠FBD+∠FBA=∠FDA+∠DAF=45°,∠ADF=2∠FAD,
∴∠FDA=30°,∠FAD=15°,
∵∠AFN=∠FAD=15°,
∴∠FNM=30°,
又∵FM⊥AD,
∴NM=![]() FM,FN=2MF=AN,
FM,FN=2MF=AN,
∴AM=AN+MN=(2+![]() )FM,
)FM,
∴tan∠FAD=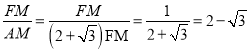 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一张三角形纸片ABC,其中∠C=90,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,点E在边AB上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P是线段AD上一动点,当半径为5的⊙P与△ABC的一边相切时,AP的长为_____.
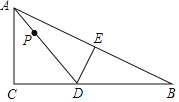
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 两点的坐标分别为
两点的坐标分别为![]() ,点
,点![]() 分别是直线
分别是直线![]() 和x轴上的动点,
和x轴上的动点,![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() 交
交![]() 轴于点
轴于点![]() ;当⊿
;当⊿![]() 面积取得最小值时,
面积取得最小值时,![]() 的值是( )
的值是( )
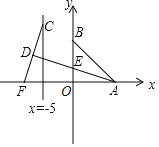
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】110年前,中国首条自行设计和建造的铁路,京张铁路落成;110年后,在同样的地方,世界首条智能高铁京张高铁正式运行,中国速度,一直在路上,2019年底,中国高铁里程将突破3.5万公里,全世界超过![]() 的高铁轨道铺设在中国.为你骄傲,中国高铁!请将3.5万公里中的数“3.5万”用科学记数法表示为( )
的高铁轨道铺设在中国.为你骄傲,中国高铁!请将3.5万公里中的数“3.5万”用科学记数法表示为( )
A.3.5×101B.0.35×105C.35×103D.3.5×104
查看答案和解析>>
科目:初中数学 来源: 题型:
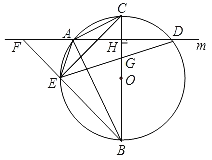
【题目】如图,在⊙O的内接△ABC中,∠CAB=90°,AB=2AC,过点A作BC的垂线m交⊙O于另一点D,垂足为H,点E为![]() 上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
(1)求证:△FED∽△AEB;
(2)若![]() =
=![]() ,AC=2,连接CE,求AE的长;
,AC=2,连接CE,求AE的长;
(3)在点E运动过程中,若BG=![]() CG,求tan∠CBF的值.
CG,求tan∠CBF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1)在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(2)甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?

查看答案和解析>>
科目:初中数学 来源: 题型:
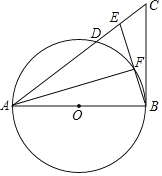
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:EF=BF;
(2)求证:BC是⊙O的切线.
(3)若AB=4,BC=3,求DE的长,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com