
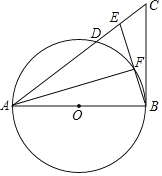
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:EF=BF;
(2)求证:BC是⊙O的切线.
(3)若AB=4,BC=3,求DE的长,
【答案】(1)见解析;(2)见解析;(3)0.8.
【解析】
根据三角形ABF中AB 为圆的直径,且点F为圆上的点,则AF与BF垂直可解答第一问;根据第一问中的AF与BF垂直,还有题意中的∠BAC=2∠CBE可以证明∠ABD为直角;根据图中的△ABD∽△ACB直接可以解答第三问.
(1)证明:∵AE=AB,
∴△ABE是等腰三角形,
∵AB为⊙O的直径,
∴AF⊥BE,
∴EF=BF;
(2)证明:∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=![]() (180°﹣∠BAC=)=90°﹣
(180°﹣∠BAC=)=90°﹣![]() ∠BAC,
∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=![]() ∠BAC,
∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣![]() ∠BAC)+
∠BAC)+![]() ∠BAC=90°,
∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
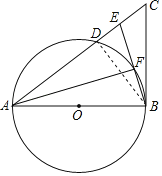
(3)解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴![]() ,
,
∵在Rt△ABC中,AB=4,BC=3,
∴AC=![]() =5,
=5,
∴![]()
AD=3.2,
∵AE=AB=4,
∴DE=AE﹣AD=4﹣3.2=0.8.


科目:初中数学 来源: 题型:
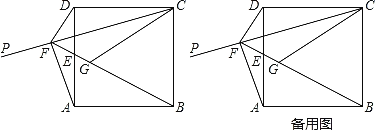
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
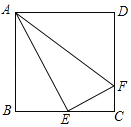
【题目】如图所示,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,下列结论:①∠BAE=30°;②△ABE∽△AEF;③CD=3CF;④S△ABE=4S△ECF.其中正确的有_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() 、
、![]() .
.
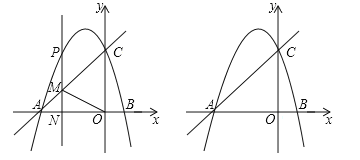
(1)求抛物线的解析式;
(2)![]() 是抛物线上一动点,过
是抛物线上一动点,过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求
为顶点的四边形是平行四边形,求![]() 的值.
的值.
②当射线![]() 、
、![]() 、
、![]() 中一条射线平分另外两条射线的夹角时,直接写出
中一条射线平分另外两条射线的夹角时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com