
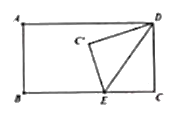
【题目】在矩形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,连接
上,连接![]() 将
将![]() 沿
沿![]() 折叠,若点
折叠,若点![]() 的对称点
的对称点![]() 到
到![]() 的距离为
的距离为![]() ,则
,则![]() 的长为______________________.
的长为______________________.
【答案】![]() 或
或![]()
【解析】
分两种情况进行分类讨论:(1)当![]() 在矩形内部到AD的距离为1;(2)点
在矩形内部到AD的距离为1;(2)点![]() 在矩形外部到AD的距离为1.
在矩形外部到AD的距离为1.
解:设CE=x.
当C在矩形内部时,如图,过点C作FG垂直AD,交AD于点F,BC于点G.
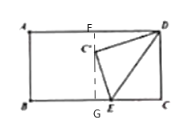
由折叠的性质,得D![]() =DC=2,∠
=DC=2,∠![]() =90°,CE=
=90°,CE=![]() E.
E.
在Rt△D![]() F中,F
F中,F![]() =1,由勾股定理,得DF=
=1,由勾股定理,得DF=![]() =
=![]() .
.
又∵∠G![]() E=∠FD
E=∠FD![]() ,∠
,∠![]() GE=∠
GE=∠![]() FD=90°,
FD=90°,
∴△G![]() E
E![]() △FD
△FD![]() ,∴
,∴![]() =
=![]() .
.
∴x=![]() .
.
当C在矩形内部时,如图,过点C’作BC的平行线,交CD的延长线G,过点E作EQ⊥QG于点Q,则EQ=2+1=3,DG=1.
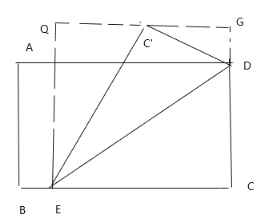
由折叠的性质,得EC’=CE,C’D=CD=2.
在Rt△D![]() G中,DG =1,由勾股定理,得C’G=
G中,DG =1,由勾股定理,得C’G=![]() =
=![]() .
.
∵∠QEC’=∠GC’D,∠Q=∠G,
∴△Q![]() E
E![]() △GD
△GD![]() ,
,![]() =
=![]() .
.
∴x=2![]() .
.
∴CE的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
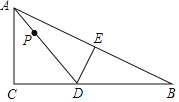
【题目】如图,Rt△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,点E在边AB上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P是线段AD上一动点,当半径为5的⊙P与△ABC的一边相切时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1)在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(2)甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售甲、乙两种品牌的A4多功能办公用纸,购买2包甲品牌和3包乙品牌的A4多功能办公用纸共需156元;购买3包甲品牌和1包乙品牌的A4多功能办公用共需122元.
(1)求这两种品牌的A4多功能办公用纸每包的单价;
(2)疫情期间,为满足师生的用纸要求,该商店对这两种A4多功能办公用纸展开了促销活动,具体办法如下:甲品牌的A4多功能办公用纸按原价的八折销售,乙品牌的A4多功能办公用纸超出5包的部分按原价的七折销售,设购买的x包甲品牌的A4多功能办公用纸需要y1元,购买x包乙品牌的A4多功能办公用纸需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50包A4多功能办公用纸时,买哪种品牌的A4多功能办公用纸更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接疫情彻底结束后的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表
运动鞋价格 | 甲 | 乙 |
进价(元/双) |
|
|
售价(元/双) |
|
|
已知:用![]() 元购进甲种运动鞋的数量与用
元购进甲种运动鞋的数量与用![]() 元购进乙种运动鞋的数量相同.
元购进乙种运动鞋的数量相同.
![]() 求
求![]() 的值;
的值;
![]() 要使购进的甲、乙两种运动鞋共
要使购进的甲、乙两种运动鞋共![]() 双的总利润(利润
双的总利润(利润![]() 售价
售价![]() 进价)不少于
进价)不少于![]() 元,且甲种运动鞋的数量不超过
元,且甲种运动鞋的数量不超过![]() 双,问该专卖店共有几种进货方案;
双,问该专卖店共有几种进货方案;
![]() 在
在![]() 的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠
的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠![]() 元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了![]() .
.
(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为![]() 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
查看答案和解析>>
科目:初中数学 来源: 题型:
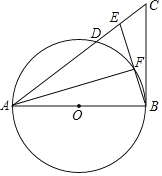
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:EF=BF;
(2)求证:BC是⊙O的切线.
(3)若AB=4,BC=3,求DE的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() …按此规律,抛物线
…按此规律,抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() (其中n为正整数),我们把抛物线
(其中n为正整数),我们把抛物线![]() 称为系数为
称为系数为![]() 的“关于原点位似”的抛物线族.
的“关于原点位似”的抛物线族.
(1)试求出![]() 的值;
的值;
(2)请用含n的代数式表示线段![]() 的长;
的长;
(3)探究下列问题:
①抛物线![]() 的顶点纵坐标
的顶点纵坐标![]() 与a、n有何数量关系?请说明理由;
与a、n有何数量关系?请说明理由;
②若系数为a的“关于原点位似”的抛物线族的各顶点坐标记为(T,S),请直接写出S和T所满足的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com