
【题目】为了迎接疫情彻底结束后的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表
运动鞋价格 | 甲 | 乙 |
进价(元/双) |
|
|
售价(元/双) |
|
|
已知:用![]() 元购进甲种运动鞋的数量与用
元购进甲种运动鞋的数量与用![]() 元购进乙种运动鞋的数量相同.
元购进乙种运动鞋的数量相同.
![]() 求
求![]() 的值;
的值;
![]() 要使购进的甲、乙两种运动鞋共
要使购进的甲、乙两种运动鞋共![]() 双的总利润(利润
双的总利润(利润![]() 售价
售价![]() 进价)不少于
进价)不少于![]() 元,且甲种运动鞋的数量不超过
元,且甲种运动鞋的数量不超过![]() 双,问该专卖店共有几种进货方案;
双,问该专卖店共有几种进货方案;
![]() 在
在![]() 的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠
的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠![]() 元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
【答案】(1)![]() ;(2)共有
;(2)共有![]() 种方案;(3)此时应购进甲种运动鞋
种方案;(3)此时应购进甲种运动鞋![]() 双,购进乙种运动鞋
双,购进乙种运动鞋![]() 双
双
【解析】
(1)用总价除以单价表示出购进鞋的数量,根据两种鞋的数量相等列出方程求解即可;
(2)设购进甲种运动鞋x双,表示出乙种运动鞋(200-x)双,然后根据总利润列出一元一次不等式组,求出不等式组的解集后,再根据鞋的双数是正整数解答;
(3)设总利润为W,根据总利润等于两种鞋的利润之和列式整理,然后根据一次函数的增减性分情况讨论求解即可.
解:![]() 依题意得,
依题意得,
![]()
整理得,![]()
解得![]()
经检验,![]() 是原分式方程的解,
是原分式方程的解,
所以,![]() ;
;
![]() 设购进甲种运动鞋
设购进甲种运动鞋![]() 双,则乙种运动鞋
双,则乙种运动鞋![]() 双,
双,
根据题意得,![]() ,
,
解得![]()
![]() 是正整数,
是正整数,
![]()
![]() 共有
共有![]() 种方案;
种方案;
![]() 设总利润为
设总利润为![]()
则![]()
当![]() 时,
时,![]() 随
随![]() 的增大而减小,
的增大而减小,
所以,当![]() 时,
时,![]() 有最大值,
有最大值,
即此时应购进甲种运动鞋![]() 双,购进乙种运动鞋
双,购进乙种运动鞋![]() 双.
双.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
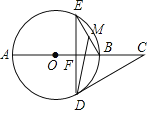
【题目】如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F,交⊙O于点E,点M是BE的中点,AB=4,∠E=∠C=30°.
(1)求证:CD是⊙O的切线;
(2)求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是多少元(用含x的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?
【答案】(1)x+10元;(2)每个定价为70元,应进货200个.(3)每个定价为65元时得最大利润,可获得的最大利润是6250元.
【解析】试题分析:(1)根据利润=销售价-进价列关系式,(2)总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍,(3)利用函数的性质求最值.
试题解析:由题意得:(1)50+x-40=x+10(元),
(2)设每个定价增加x元,
列出方程为:(x+10)(400-10x)=6000,解得:x1=10,x2=20,要使进货量较少,则每个定价为70元,应进货200个,
(3)设每个定价增加x元,获得利润为y元,
y=(x+10)(400-10x)=-10x2+300x+4000=-10(x-15)2+6250,当x=15时,y有最大值为6250,所以每个定价为65元时得最大利润,可获得的最大利润是6250元.
【题型】解答题
【结束】
24
【题目】猜想与证明:
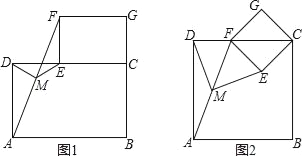
如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,某校九年级同学对“新冠疫情下停课不停学”线上学习的家长进行问卷调查,随机调查了若干名家长对线上学习的态度(态度分为:A.无所谓;B.基本赞成;C.反对;D.赞成).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
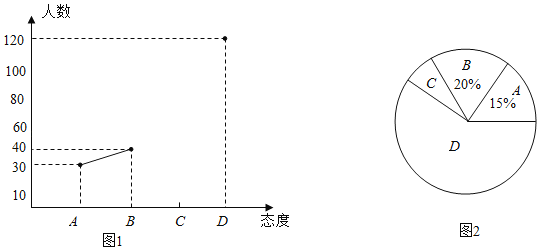
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对线上学习,持基本赞成的态度,初三(2)班有B1、B2两位学生家长对线上学习,也持基本赞成的态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 | 90<x≤100 | 8 |
第2组 | 80<x≤90 | a |
第3组 | 70<x≤80 | 10 |
第4组 | 60<x≤70 | b |
第5组 | 50<x≤60 | 3 |
请根据以上信息,解答下列问题:

(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
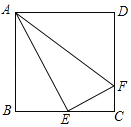
【题目】如图所示,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,下列结论:①∠BAE=30°;②△ABE∽△AEF;③CD=3CF;④S△ABE=4S△ECF.其中正确的有_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
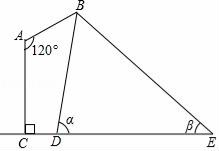
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com