
【题目】目前,某校九年级同学对“新冠疫情下停课不停学”线上学习的家长进行问卷调查,随机调查了若干名家长对线上学习的态度(态度分为:A.无所谓;B.基本赞成;C.反对;D.赞成).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
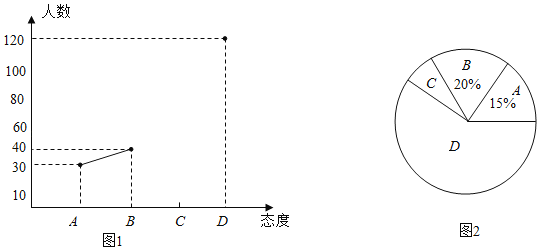
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对线上学习,持基本赞成的态度,初三(2)班有B1、B2两位学生家长对线上学习,也持基本赞成的态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
【答案】(1)200名;(2)18°,补图见解析;(3)![]() .
.
【解析】
(1)用A类人数除以它所占的百分比得到调查的总人数;
(2)先计算出C类的人数,再利用360°乘以C类人数所占的百分比得到图2中扇形C所对的圆心角度数,然后补全频数折线统计图;
(3)画树状图展示所有12种等可能的结果数,找出选出的2人来自不同班级的结果数,然后根据概率公式求解.
解:(1)30÷15%=200,
所以共调查了200名中学生家长;
(2)C类人数为200﹣30﹣40﹣120=10(人),
所以扇形C所对的圆心角度数=360°×![]() =18°;
=18°;
频数折线统计图为:

(3)画树状图为:
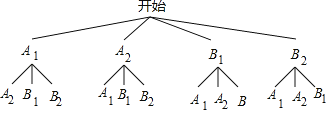
共有12种等可能的结果数,其中选出的2人来自不同班级的结果数为8,
所以选出的2人来自不同班级的概率=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
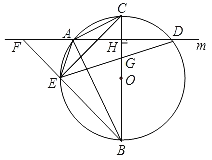
【题目】如图,在⊙O的内接△ABC中,∠CAB=90°,AB=2AC,过点A作BC的垂线m交⊙O于另一点D,垂足为H,点E为![]() 上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
(1)求证:△FED∽△AEB;
(2)若![]() =
=![]() ,AC=2,连接CE,求AE的长;
,AC=2,连接CE,求AE的长;
(3)在点E运动过程中,若BG=![]() CG,求tan∠CBF的值.
CG,求tan∠CBF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解在校初中生阅读数学文化史类书籍的现状,随机抽取了初中部部分学生进行研究调查,依据相关数据绘制成以下不完整的的统计图表,请你根据图表中的信息解答下列问题:
类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | C |
说不清楚 | 9 | 0.06 |
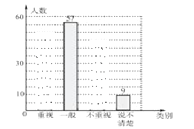
(1)求表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2400名,请估计该校“不重视”阅读数学文化史书籍的初中生人数;
(3)若小明和小华去书店,打算从A,B,C,D四本数学文化史类书籍中随机选取一本,请用画树状图或列表格的方法,求两人恰好选中同一本书籍的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1)在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(2)甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠B=60°,动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B,同时动点Q以每秒2个单位的速度自点B出发沿折线B﹣C﹣D运动到点D.图2是点P、Q运动时,△BPQ的面积S随时间t变化关系图象,则a的值是( )
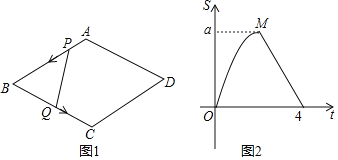
A.2B.2.5C.3D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接疫情彻底结束后的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表
运动鞋价格 | 甲 | 乙 |
进价(元/双) |
|
|
售价(元/双) |
|
|
已知:用![]() 元购进甲种运动鞋的数量与用
元购进甲种运动鞋的数量与用![]() 元购进乙种运动鞋的数量相同.
元购进乙种运动鞋的数量相同.
![]() 求
求![]() 的值;
的值;
![]() 要使购进的甲、乙两种运动鞋共
要使购进的甲、乙两种运动鞋共![]() 双的总利润(利润
双的总利润(利润![]() 售价
售价![]() 进价)不少于
进价)不少于![]() 元,且甲种运动鞋的数量不超过
元,且甲种运动鞋的数量不超过![]() 双,问该专卖店共有几种进货方案;
双,问该专卖店共有几种进货方案;
![]() 在
在![]() 的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠
的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠![]() 元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.如图,抛物线C1与抛物线C2组成一个开口向上的“月牙线”,抛物线C1与抛物线C2与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx﹣12m,(m>0).
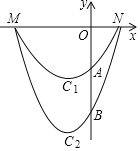
(1)请你根据“月牙线”的定义,设计一个开口向下.“月牙线”,直接写出两条抛物线的解析式;
(2)求M,N两点的坐标;
(3)在第三象限内的抛物线C1上是否存在一点P,使得△PAM的面积最大?若存在,求出△PAM的面积的最大值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】事业单位人员编制连进必考,现一事业单位需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方而进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 84 | 80 | 88 |
乙 | 94 | 92 | 69 |
丙 | 81 | 84 | 78 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该单位规定:笔试、面试、体能分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com