
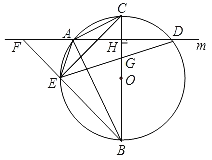
【题目】如图,在⊙O的内接△ABC中,∠CAB=90°,AB=2AC,过点A作BC的垂线m交⊙O于另一点D,垂足为H,点E为![]() 上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
(1)求证:△FED∽△AEB;
(2)若![]() =
=![]() ,AC=2,连接CE,求AE的长;
,AC=2,连接CE,求AE的长;
(3)在点E运动过程中,若BG=![]() CG,求tan∠CBF的值.
CG,求tan∠CBF的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据同角的余角重叠得出∠EAB=∠ECB,然后根据三角形相似的判定定理判定即可得出结论;
(2)根据相交弦定理得出DH=AH=![]() ,再根据勾股定理得,BH=
,再根据勾股定理得,BH=![]() ,进而求出BE=CE=
,进而求出BE=CE=![]() ,进而求出EF=
,进而求出EF=![]() ,FD=
,FD=![]() ,借助(1)的结论即可得出结论;
,借助(1)的结论即可得出结论;
(3)根据平行线分线段成比例得出判![]() ,根据平行线的性质得出tan∠CBF=tan∠CGT=
,根据平行线的性质得出tan∠CBF=tan∠CGT=![]() ,根据圆周角定理得出tan∠CED=tan∠ABC,进而得出
,根据圆周角定理得出tan∠CED=tan∠ABC,进而得出![]() ,再结合已知条件
,再结合已知条件![]() ,即可得出结论.
,即可得出结论.
解:(1)∵⊙O的内接△ABC中,∠CAB=90°,
∴BC是⊙O的直径,
∵点E为![]() 上异于A,B的一个动点,
上异于A,B的一个动点,
∴∠CEB=90°,
∴∠ECB+∠EBC=90°,
∵过点A作BC的垂线m交⊙O于另一点D,垂足为H,
∴∠FHB=90°,
∴∠FBH+∠HFB=90°,
∴∠HFB=∠ECB,
∵∠EAB=∠ECB,
∴∠EAB=∠HFB,
∵∠FBA=∠ADE,
∴△FED∽△AEB;
(2)∵∠CAB=90°,AB=2AC,AC=2,
∴AB=4,
根据勾股定理得,BC=2![]() ,
,
∵AD⊥BC,BC是⊙O的切线,
∴DH=AH=![]() =
=![]() =
=![]() ,
,
在Rt△AHB中,根据勾股定理得,BH=![]() =
=![]() ,
,
∵![]() ,BC是⊙O的直径,
,BC是⊙O的直径,
∴BE=CE,∠ECB=∠EBC=45°,
∵BC=2![]() ,∠BEC=90°,
,∠BEC=90°,
∴BE=CE=![]() ,
,
∵∠FHB=90°,∠EBC=45°,BH=![]() ,
,
∴FH=BH=![]() ,BF=
,BF=![]() ,
,
∴EF=BF﹣BE=![]() ,FD=FH+DH=
,FD=FH+DH=![]() ,
,
∵△FED∽△AEB,
∴![]() ,
,
∴ ,
,
∴AE=![]() ;
;
(3)如图,过点G作GT⊥CE于T,

∵∠CEB=90°,
∴TG∥EB,
∴![]() ,∠CGT=∠CBF,
,∠CGT=∠CBF,
∴tan∠CBF=tan∠CGT=![]() ,
,
∵![]() ,
,
∴∠CED=∠ABC,
∴tan∠CED=tan∠ABC,
∴![]() ,
,
∵![]() ,BG=
,BG=![]() CG,
CG,
∴ET=![]() CT,
CT,![]() ,
,
∴![]() ,
,
∴tan∠CBF=tan∠CGT=![]() .
.


科目:初中数学 来源: 题型:
【题目】某市水果批发欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时,其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1) 如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.(总支出包含损耗、运费和装卸费用)
(2) 如果A市与B市之间的距离为S千米,你若是A市水果批发部门的经理,要想将这种水果运往B市销售,试分析以上两种运输工具中选择哪种运输方式比较合算呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
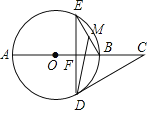
【题目】如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F,交⊙O于点E,点M是BE的中点,AB=4,∠E=∠C=30°.
(1)求证:CD是⊙O的切线;
(2)求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
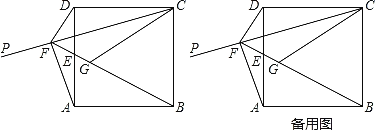
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
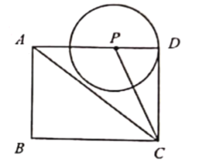
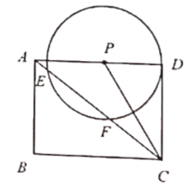
【题目】如图1,在矩形![]() 中,
中,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,以点
上的一个动点,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,连接
,连接![]() .
.
(1)当![]() 经过
经过![]() 的中点时,
的中点时,![]() 的长为_ ;
的长为_ ;
(2)当![]() 平分
平分![]() 时,判断
时,判断![]() 与
与![]() 的位置关系.说明理由,并求出
的位置关系.说明理由,并求出![]() 的长;
的长;
(3)如图2,当![]() 与
与![]() 交于
交于![]() 两点,且
两点,且![]() 时,求点
时,求点![]() 到
到![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是多少元(用含x的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?
【答案】(1)x+10元;(2)每个定价为70元,应进货200个.(3)每个定价为65元时得最大利润,可获得的最大利润是6250元.
【解析】试题分析:(1)根据利润=销售价-进价列关系式,(2)总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍,(3)利用函数的性质求最值.
试题解析:由题意得:(1)50+x-40=x+10(元),
(2)设每个定价增加x元,
列出方程为:(x+10)(400-10x)=6000,解得:x1=10,x2=20,要使进货量较少,则每个定价为70元,应进货200个,
(3)设每个定价增加x元,获得利润为y元,
y=(x+10)(400-10x)=-10x2+300x+4000=-10(x-15)2+6250,当x=15时,y有最大值为6250,所以每个定价为65元时得最大利润,可获得的最大利润是6250元.
【题型】解答题
【结束】
24
【题目】猜想与证明:
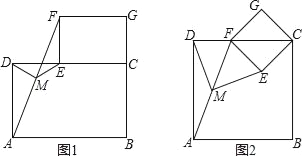
如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,某校九年级同学对“新冠疫情下停课不停学”线上学习的家长进行问卷调查,随机调查了若干名家长对线上学习的态度(态度分为:A.无所谓;B.基本赞成;C.反对;D.赞成).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
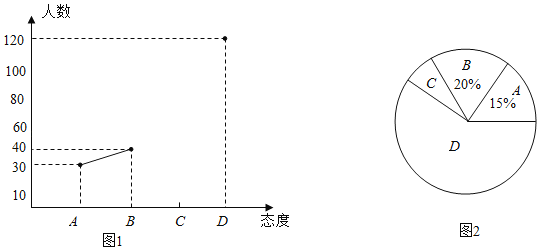
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对线上学习,持基本赞成的态度,初三(2)班有B1、B2两位学生家长对线上学习,也持基本赞成的态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com