
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,若
,若![]() 为锐角,则
为锐角,则![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]() 或
或![]() 且
且![]()
【解析】
先求出点A及B、C的坐标,再分两种情况讨论:当点A、B在原点两侧时,利用∠ACB是直角求出m=-1,即可得到m<-1;当点A、B在原点同侧时,∠ACB始终是锐角,得到m>0且![]() .
.
令![]() 中y=0,得到
中y=0,得到![]() ,
,![]() ,
,
∴点A的坐标为(m,0),点B的坐标为(1,0),
当x=0时,y=m,
∴点C的坐标为(0,m),
当点A、B在原点两侧时,如图,若∠ACB=90°,
∵OA=OC,
∴∠ACO=45°,
∴∠BCO=45°,
∴OC=OB=1,即m=-1,
∴当m<-1时,∠ACB是锐角;
当点A、B在原点同侧时,∠ACB是锐角,此时m>0,
当m=1时,抛物线与x轴只有一个交点,故![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() 或
或![]() 且
且![]() .
.
 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解初中学生参加综合实践活动的情况,随机抽取了本市初一、初二、初三年级各![]() 名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.

(1)在被调查的学生中,参加综合实践活动的有多少人,参加科技活动的有多少人;
(2)如果本市有![]() 万名初中学生,请你估计参加科技活动的学生约有多少名.
万名初中学生,请你估计参加科技活动的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时,其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1) 如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.(总支出包含损耗、运费和装卸费用)
(2) 如果A市与B市之间的距离为S千米,你若是A市水果批发部门的经理,要想将这种水果运往B市销售,试分析以上两种运输工具中选择哪种运输方式比较合算呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,以点
上的一个动点,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,连接
,连接![]() .
.
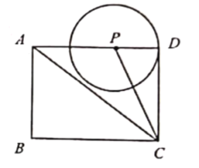
(1)当![]() 经过
经过![]() 的中点时,
的中点时,![]() 的长为_ ;
的长为_ ;
(2)当![]() 平分
平分![]() 时,判断
时,判断![]() 与
与![]() 的位置关系.说明理由,并求出
的位置关系.说明理由,并求出![]() 的长;
的长;
(3)如图2,当![]() 与
与![]() 交于
交于![]() 两点,且
两点,且![]() 时,求点
时,求点![]() 到
到![]() 的距离.
的距离.
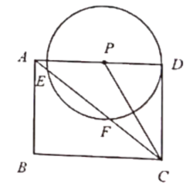
查看答案和解析>>
科目:初中数学 来源: 题型:
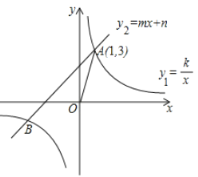
【题目】如图,反比例函数![]() 和一次函数
和一次函数![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求一次函数和反比例函数解析式;
(2)连接OA,试问在x轴上是否存在点P,使得![]() 为以OA为腰的等腰三角形,若存在,直接写出满足题意的点P的坐标;若不存在,说明理由.
为以OA为腰的等腰三角形,若存在,直接写出满足题意的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为4,E、F、G、H分别是AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能是( )
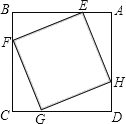
A.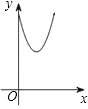 B.
B.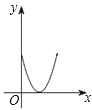
C.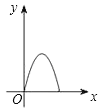 D.
D.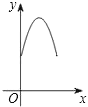
查看答案和解析>>
科目:初中数学 来源: 题型:
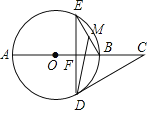
【题目】如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F,交⊙O于点E,点M是BE的中点,AB=4,∠E=∠C=30°.
(1)求证:CD是⊙O的切线;
(2)求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,某校九年级同学对“新冠疫情下停课不停学”线上学习的家长进行问卷调查,随机调查了若干名家长对线上学习的态度(态度分为:A.无所谓;B.基本赞成;C.反对;D.赞成).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
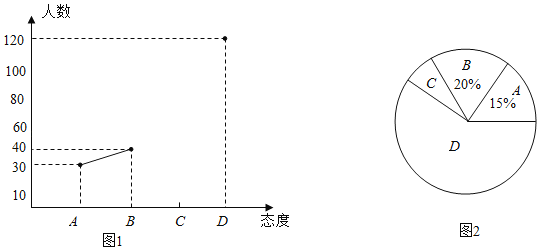
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对线上学习,持基本赞成的态度,初三(2)班有B1、B2两位学生家长对线上学习,也持基本赞成的态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com