
ЁОЬтФПЁПвбжЊХзЮяЯп![]() НЛ
НЛ![]() жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу
жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу
жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу
жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу![]() ЁАДДЫЙцТЩЃЌХзЮяЯп
ЁАДДЫЙцТЩЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу
жсгкЕуЃЈ0ЃЌ0ЃЉКЭЕу![]() ЃЈЦфжаnЮЊе§ећЪ§ЃЉЃЌЮвУЧАбХзЮяЯп
ЃЈЦфжаnЮЊе§ећЪ§ЃЉЃЌЮвУЧАбХзЮяЯп![]() ГЦЮЊЯЕЪ§ЮЊ
ГЦЮЊЯЕЪ§ЮЊ![]() ЕФЁАЙигкдЕуЮЛЫЦЁБЕФХзЮяЯпзхЃЎ
ЕФЁАЙигкдЕуЮЛЫЦЁБЕФХзЮяЯпзхЃЎ
ЃЈ1ЃЉЪдЧѓГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧыгУКЌnЕФДњЪ§ЪНБэЪОЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉЬНОПЯТСаЮЪЬтЃК
ЂйХзЮяЯп![]() ЕФЖЅЕузнзјБъ
ЕФЖЅЕузнзјБъ![]() гыaЁЂnгаКЮЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
гыaЁЂnгаКЮЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЂкШєЯЕЪ§ЮЊaЕФЁАЙигкдЕуЮЛЫЦЁБЕФХзЮяЯпзхЕФИїЖЅЕузјБъМЧЮЊЃЈTЃЌSЃЉЃЌЧыжБНгаДГіSКЭTЫљТњзуЕФКЏЪ§ЙиЯЕЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2 ЃЈ2ЃЉ![]() ЃЈ3ЃЉЂйМћНтЮі Ђк
ЃЈ3ЃЉЂйМћНтЮі Ђк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнХзЮяЯпC1ЃКy1=a(x-1)2+k1ЃЈaЁй0ЃЉНЛxжсгкЕуЃЈ0ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпx=1ЃЌПЩЕУХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЃЌНјвЛВНЕУЕНb1ЕФжЕЃЛ
ЃЈ2ЃЉгЩгыЃЈ1ЃЉЯрЭЌЕФЗНЗЈПЩЕУbn=2nЃЌдђAn-1An=bn-bn-1ПЩЧѓЃЛ
ЃЈ3ЃЉЂйгЩЃЈ1ЃЉЭЌбљЕФЗНЗЈПЩжЊЃЌk3=-16aЃЌk4=-64aЃЌАДДЫЙцТЩПЩжЊЃЌknгыaЁЂnЕФЪ§СПЙиЯЕЃЛ
ЂкИљОнХзЮяЯпзхЕФЖЅЕузјБъSКЭTжЎМфЕФЙиЯЕМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпC1ЃКy1=aЃЈxЉ1ЃЉ2+k1ЃЈaЁй0ЃЉНЛxжсгкЕуЃЈ0ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпx=1ЃЌ
ЁрХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊЃЈ2ЃЌ0ЃЉЃЌ
Ёрb1=2ЃЎ
ЙЪД№АИЮЊЃК2.
ЃЈ2ЃЉгЩгыЃЈ1ЃЉЯрЭЌЕФЗНЗЈПЩЕУb2=4ЃЌb3=8ЃЌb4=16ЃЌ
АДДЫЙцТЩПЩЕУbn=2nЃЌ
ЁрAnЉ1An=bnЉbnЉ1=2nЉ2nЉ1=2nЉ1ЃЎ
ЙЪД№АИЮЊЃК2nЉ1
ЃЈ3ЃЉЂйknгыaЁЂnЕФЪ§СПЙиЯЕЮЊЃКkn=Љ4nЉ1aЃЌ
РэгЩШчЯТЃКгЩЃЈ1ЃЉНЋЃЈ0ЃЌ0ЃЉДњШыy1=aЃЈxЉ1ЃЉ2+k1ЃЌПЩЕУk1=ЉaЃЌ
Ёпb1=2ЃЌ
ЁрC2ЃКy2=aЃЈxЉb1ЃЉ2+k2ПЩЛЏЮЊC2ЃКy2=aЃЈxЉ2ЃЉ2+k2ЃЌ
ЁпХзЮяЯпC2ЃКy2=aЃЈxЉ2ЃЉ2+k2НЛxжсгыЕуЃЈ0ЃЌ0ЃЉЃЌ
Ёр0=aЃЈ0Љ2ЃЉ2+k2ЃЌ
Ёр4a+k2=0ЃЌМДk2=Љ4aЃЎ
гУЭЌбљЕФЗНЗЈПЩжЊЃЌk3=Љ16aЃЌk4=Љ64aЃЌ
АДДЫЙцТЩПЩжЊЃЌknгыaЁЂnЕФЪ§СПЙиЯЕЮЊЃКkn=Љ4nЉ1a
ЙЪД№АИЮЊЃКkn=Љ4nЉ1a.
ЂкгЩЩЯЪіПЩжЊЃК![]() ЕФЖЅЕузјБъЮЊЃК
ЕФЖЅЕузјБъЮЊЃК![]()
Цфжа![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
ХзЮяЯпзхЕФЖЅЕузјБъSКЭTЫљТњзуЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() .
.
ЙЪД№АИЮЊЃК![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() НЋ
НЋ![]() би
би![]() елЕўЃЌШєЕу
елЕўЃЌШєЕу![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЕН
ЕН![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊ______________________ЃЎ
ЕФГЄЮЊ______________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎжБЯп
ЃЎжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
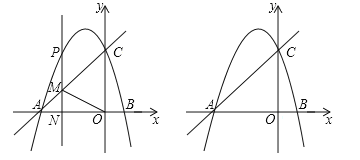
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉ![]() ЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§
ЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§![]() зї
зї![]() жсНЛжБЯп
жсНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
ЂйШєвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЂкЕБЩфЯп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() жавЛЬѕЩфЯпЦНЗжСэЭтСНЬѕЩфЯпЕФМаНЧЪБЃЌжБНгаДГі
жавЛЬѕЩфЯпЦНЗжСэЭтСНЬѕЩфЯпЕФМаНЧЪБЃЌжБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
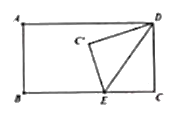
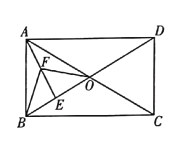
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЦНааЫФБпаЮABCDЃЌЖдНЧЯпACгыBDЯрНЛгкЕуEЃЌЕуGЮЊADЕФжаЕуЃЌСЌНгCGЃЌCGЕФбгГЄЯпНЛBAЕФбгГЄЯпгкЕуFЃЌСЌНгFDЃЎ
ЃЈ1ЃЉЧѓжЄЃКAB=AFЃЛ
ЃЈ2ЃЉШєAG=ABЃЌЁЯBCD=120ЁуЃЌХаЖЯЫФБпаЮACDFЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊЩшСЫЁА3DЁБДђгЁЁЂЪ§бЇЪЗЁЂЪЋИшаРЩЭЁЂЬевежЦзїЫФУХаЃБОПЮГЬЃЌЮЊСЫНтбЇЩњЖдетЫФУХаЃБОПЮГЬЕФЯВАЎЧщПіЃЌЖдбЇЩњНјааСЫЫцЛњЮЪОэЕїВщЃЈЮЪОэЕїВщБэШчЭМЫљЪОЃЉЃЌНЋЕїВщНсЙћећРэКѓЛцжЦР§ЭМ1ЁЂЭМ2СНЗљОљВЛЭъећЕФЭГМЦЭМБэЃЎ
аЃБОПЮГЬ | ЁЁЦЕЪ§ | ЁЁЦЕТЪ |
A | 36 | 0.45 |
B | ЁЁ | 0.25 |
C | 16 | b |
D | 8 | ЁЁ |
ЁЁКЯМЦ | a | 1 |
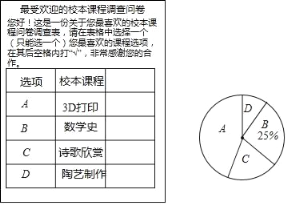
ЧыФњИљОнЭМБэжаЬсЙЉЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭГМЦБэжаЕФaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЁАDЁБЖдгІЩШаЮЕФдВаФНЧЮЊЁЁ ЁЁЖШЃЛ
ЃЈ3ЃЉИљОнЕїВщНсЙћЃЌЧыФњЙРМЦИУаЃ2000УћбЇЩњжазюЯВЛЖЁАЪ§бЇЪЗЁБаЃБОПЮГЬЕФШЫЪ§ЃЛ
ЃЈ4ЃЉаЁУїКЭаЁССВЮМгаЃБОПЮГЬбЇЯАЃЌШєУПШЫДгЁАAЁБЁЂЁАBЁБЁЂЁАCЁБШ§УХаЃБОПЮГЬжаЫцЛњбЁШЁвЛУХЃЌЧыгУЛЪїзДЭМЛђСаБэИёЕФЗНЗЈЃЌЧѓСНШЫЧЁКУбЁжаЭЌвЛУХаЃБОПЮГЬЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
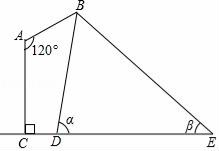
ЁОЬтФПЁПШчЭМЪЧФГТЗЕЦдкЧІДЙУцФкЕФЪОвтЭМЃЌЕЦжљACЕФИпЮЊ11УзЃЌЕЦИЫABгыЕЦжљACЕФМаНЧЁЯA=120ЁуЃЌТЗЕЦВЩгУзЖаЮЕЦежЃЌдкЕиУцЩЯЕФееЩфЧјгђDEГЄЮЊ18УзЃЌДгDЃЌEСНДІВтЕУТЗЕЦBЕФбіНЧЗжБ№ЮЊІСКЭІТЃЌЧвtanІС=6ЃЌtanІТ=![]() ЃЌЧѓЕЦИЫABЕФГЄЖШЃЎ
ЃЌЧѓЕЦИЫABЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧАыдВOЕФжБОЖЃЌЩфЯпAMЁЭABЃЌЕуPдкAMЩЯЃЌСЌНгOPНЛАыдВOгкЕуDЃЌPCЧаАыдВOгкЕуCЃЌСЌНгBCЃЌOCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїOAPЁеЁїOCPЃЛ
ЃЈ2ЃЉШєАыдВOЕФАыОЖЕШгк2ЃЌЬюПеЃК
ЂйЕБAP= ЁЁ ЁЁЪБЃЌЫФБпаЮOAPCЪЧе§ЗНаЮЃЛ
ЂкЕБAP=ЁЁ ЁЁЪБЃЌЫФБпаЮBODCЪЧСтаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() ЖдНЧЯп
ЖдНЧЯп![]() НЛгкЕу
НЛгкЕу![]() ЮЊ
ЮЊ![]() ЩЯШЮвтЕуЃЌ
ЩЯШЮвтЕуЃЌ![]() ЮЊ
ЮЊ![]() жаЕуЃЌдђ
жаЕуЃЌдђ![]() ЕФзюаЁжЕЮЊЃЈ ЃЉ
ЕФзюаЁжЕЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉ![]() _________ЃЌ
_________ЃЌ![]() _________ЃЛ
_________ЃЛ
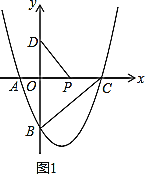
ЃЈ2ЃЉШчЭМ1ЃЌ![]() ЪЧ
ЪЧ![]() жсЩЯвЛЖЏЕуЃЌЕу
жсЩЯвЛЖЏЕуЃЌЕу![]() дк
дк![]() жсЩЯЃЌСЌНг
жсЩЯЃЌСЌНг![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
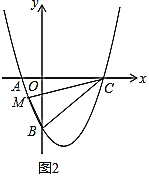
ЃЈ3ЃЉШчЭМ2ЃЌЕу![]() дкХзЮяЯпЩЯЃЌШє
дкХзЮяЯпЩЯЃЌШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com