
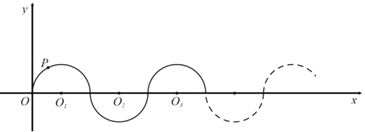
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆![]() ,
,![]() ,
,![]() ,…组成一条平滑的曲线.点
,…组成一条平滑的曲线.点![]() 从原点
从原点![]() 出发,沿这条曲线向右运动,速度为每秒
出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2002秒时点
个单位长度,则第2002秒时点![]() 的坐标为____.
的坐标为____.
【答案】![]()
【解析】
由半圆的半径以及部分点P的坐标可找出规律P8n(8n×![]() ,0)P8n+1((8n+1)×
,0)P8n+1((8n+1)×![]() ,
,![]() ),P8n+2((8n+2)×
),P8n+2((8n+2)×![]() ,1),P8n+3((8n+3)
,1),P8n+3((8n+3)![]() ,
,![]() ),P8n+4((8n+4)
),P8n+4((8n+4)![]() ,0),P8n+5((8n+5)×
,0),P8n+5((8n+5)×![]() ,-
,-![]() ),P8n+6((8n+6)×
),P8n+6((8n+6)×![]() ,-1),P8n+7((8n+7)×
,-1),P8n+7((8n+7)×![]() ,-
,-![]() ),P8n+8((8n+8)×
),P8n+8((8n+8)×![]() ,1),根据本规律即可得解答..
,1),根据本规律即可得解答..
解:以时间为点P的下标.
观察可以发现规律:P0(0,0),P1(![]() ,
,![]() ),P2(1,1),P3(1
),P2(1,1),P3(1![]() ,
,![]() ),P4(2,0),P5(5×
),P4(2,0),P5(5×![]() ,-
,-![]() ),P6(6×
),P6(6×![]() ,-1),P7(7×
,-1),P7(7×![]() ,-
,-![]() ),…P8n(8n×
),…P8n(8n×![]() ,0)P8n+1((8n+1)×
,0)P8n+1((8n+1)×![]() ,
,![]() ),P8n+2((8n+2)×
),P8n+2((8n+2)×![]() ,1),P8n+3((8n+3)
,1),P8n+3((8n+3)![]() ,
,![]() ),P8n+4((8n+4)
),P8n+4((8n+4)![]() ,0),P8n+5((8n+5)×
,0),P8n+5((8n+5)×![]() ,-
,-![]() ),P8n+6((8n+6)×
),P8n+6((8n+6)×![]() ,-1),P8n+7((8n+7)×
,-1),P8n+7((8n+7)×![]() ,-
,-![]() ),P8n+8((8n+8)×
),P8n+8((8n+8)×![]() ,1).
,1).
∵2002=8×250+2,
∴.第2002秒时,点P的坐标是(2002×![]() , 1)即(1001,1).
, 1)即(1001,1).
故答案为(1001,1).


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(1-m)x+2m-3,
(1)若函数图象经过原点,求m的值;
(2)若y随x增大而减小,求m的取值范围
(3)若函数图象平行于y=2x-3,求这个函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】师徒二人各加工同样多的零件,师父每小时加工200个,徒弟每小时加工125个.若徒弟先加工段时间之后,师父才开始工作师父工作2小时后发现自己加工的零件个数和徒弟加工的个数刚好相同,如图是师徒两人完成的零件个数之差y(个)与徒弟工作的时间x(小时)之间的函数图象,根据图象回答问题:
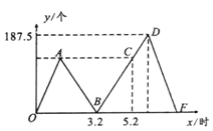
(1)求出点A的坐标,并解释该点坐标表示的实际意义;
(2)求出线段BD的函数表达式;
(3)求徒弟这次加工的零件总数
查看答案和解析>>
科目:初中数学 来源: 题型:
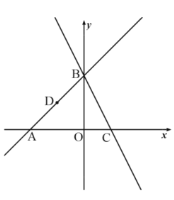
【题目】如图,![]() ,
,![]() 是直线
是直线![]() 与坐标轴的交点,直线
与坐标轴的交点,直线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() ,
,![]() 三点的坐标.
三点的坐标.
(2)当点![]() 是
是![]() 的中点时,在
的中点时,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的和最小,画出点
的和最小,画出点![]() 的位置,并求
的位置,并求![]() 点的坐标.
点的坐标.
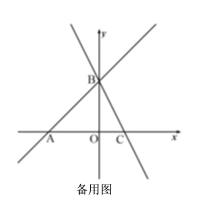
(3)若点![]() 是折线
是折线![]() 上一动点,是否存在点
上一动点,是否存在点![]() ,使
,使![]() 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
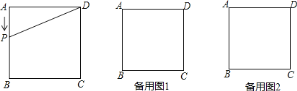
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,有一动点
,有一动点![]() 以
以![]() 的速度沿
的速度沿![]() 的路径运动,设
的路径运动,设![]() 点运动的时间为
点运动的时间为![]() ,
,![]() 的面积为
的面积为![]()
![]() .
.
![]() 当
当![]() 是等腰直角三角形时,直接写出
是等腰直角三角形时,直接写出![]() 的值.答:
的值.答:![]() ________;
________;
![]() 求
求![]() 与
与![]() 的函数关系式并写出自变量
的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com