
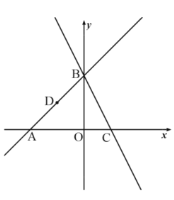
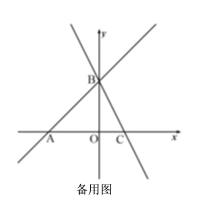
【题目】如图,![]() ,
,![]() 是直线
是直线![]() 与坐标轴的交点,直线
与坐标轴的交点,直线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() ,
,![]() 三点的坐标.
三点的坐标.
(2)当点![]() 是
是![]() 的中点时,在
的中点时,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的和最小,画出点
的和最小,画出点![]() 的位置,并求
的位置,并求![]() 点的坐标.
点的坐标.
(3)若点![]() 是折线
是折线![]() 上一动点,是否存在点
上一动点,是否存在点![]() ,使
,使![]() 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

【答案】(1)A(-4,0),B(0,4),C(2,0);(2)画图见解析;E![]() ;(3)存在,
;(3)存在,![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
【解析】
(1)分别令x=0,y=0即可确定A、B的坐标,然后确定直线BC的解析式,然后再令y=0,即可求得C的坐标;
(2)先根据中点的性质求出D的坐标,然后再根据轴对称确定![]() 的坐标,然后确定DB1的解析式,令y=0,即可求得E的坐标;
的坐标,然后确定DB1的解析式,令y=0,即可求得E的坐标;
(3)分别就D点在AB和D点BC上两种情况进行解答即可.
解:(1)在![]() 中,
中,
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
![]() ,
,![]() .
.
把![]() 代入,
代入,![]() ,
,
得![]()
![]() 直线
直线![]() 为:
为:![]() .
.
在![]() 中,
中,
令![]() ,得
,得![]() ,
,
![]() 点的坐标为
点的坐标为![]() ;
;
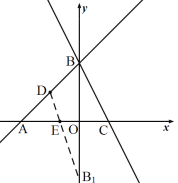
(2)如图点![]() 为所求
为所求
![]() 点
点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() .
.
![]() .
.
点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
把![]() ,
,![]() 代入,
代入,
得![]() .
.
解得![]() ,
,![]() .
.
故该直线方程为:![]() .
.
令![]() ,得
,得![]() 点的坐标为
点的坐标为![]() .
.
(3)存在,![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
①当点![]() 在
在![]() 上时,由
上时,由![]()
得到:![]() ,
,
由等腰直角三角形求得![]() 点的坐标为
点的坐标为![]() ;
;
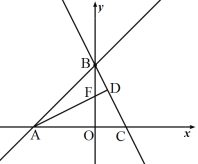
②当点![]() 在
在![]() 上时,如图,设
上时,如图,设![]() 交
交![]() 轴于点
轴于点![]() .
.
在![]() 与
与![]() 中,
中,
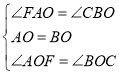
![]() .
.
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
易得直线![]() 的解析式为
的解析式为![]() ,
,
与![]() 组成方程组
组成方程组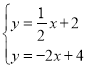 ,
,
解得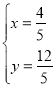 .
.
![]() 交点
交点![]() 的坐标为
的坐标为![]()


科目:初中数学 来源: 题型:
【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[-4.8]= ;
(2)已知:动点C在数轴上表示数a,且-2≤[a]≤4,则a的取值范围;
(3)求方程4x-3[x]+5=0的整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣bx+2(﹣2≤b≤2),当b从﹣2逐渐增加到2的过程中,它所对应的抛物线的位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是( )
A. 先往左上方移动,再往左下方移动
B. 先往左下方移动,再往左上方移动
C. 先往右上方移动,再往右下方移动
D. 先往右下方移动,再往右上方移动
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=2x+3与抛物线y=ax2交于A、B两点,已知点A的横坐标为3.
(1)求A、B两点的坐标及抛物线的解析式;
(2)O为坐标原点,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
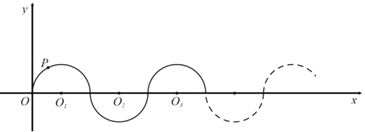
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆![]() ,
,![]() ,
,![]() ,…组成一条平滑的曲线.点
,…组成一条平滑的曲线.点![]() 从原点
从原点![]() 出发,沿这条曲线向右运动,速度为每秒
出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2002秒时点
个单位长度,则第2002秒时点![]() 的坐标为____.
的坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队同时挖掘两段长度相等的隧道,如图是甲、乙两队挖掘隧道长度![]() (米)与挖掘时间
(米)与挖掘时间![]() (时)之间关系的部分图象.请解答下列问题:
(时)之间关系的部分图象.请解答下列问题:
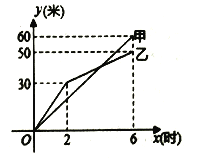
![]() 在前
在前![]() 小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
![]() ①当
①当![]() 时,求出
时,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②开挖几小时后,两工程队挖掘隧道长度相差![]() 米?
米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD//BC,∠BCD=90,对角线AC、BD相交于点E,且AC⊥BD.
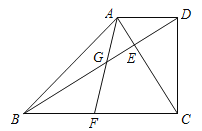
(1)求证:![]() ;
;
(2)点F是边BC上一点,联结AF,与BD相交于点G.如果∠BAF =∠DBF,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com