
【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[-4.8]= ;
(2)已知:动点C在数轴上表示数a,且-2≤[a]≤4,则a的取值范围;
(3)求方程4x-3[x]+5=0的整数解.
【答案】(1)3,-5;(2)![]() ;(3)x=-5.
;(3)x=-5.
【解析】
(1)根据新定义可得;
(2)由-2≤[a]≤4,根据[a]为不大于a的最大整数,据此可得;
(3)整理方程得[x]=![]() ,根据定义得出x-1<
,根据定义得出x-1<![]() ≤x,解不等式组求得x的取值范围,由[x]=
≤x,解不等式组求得x的取值范围,由[x]= ![]() 是整数,设4x+5=3n(n是整数)得到x=
是整数,设4x+5=3n(n是整数)得到x=![]() ,则-8<
,则-8<![]() ≤-5,解得-9<n≤-5,即可求得当n=-5,方程的整数解为x=-5.
≤-5,解得-9<n≤-5,即可求得当n=-5,方程的整数解为x=-5.
(1)∵[m]为不大于m的最大整数,
∴[3.2]=3,[-4.8]=-5
(2)∵-2≤[a]≤4,[a]为不大于a的最大整数,
∴![]() ;
;
(3)整理得:[x]= ![]()
∴x-1<![]() ≤x
≤x
解得不等式组的解集为:-8<x≤-5,
∵[x]=是整数
设4x+5=3n(n是整数)
∴x=![]() ,
,
∴-8<![]() ≤-5
≤-5
解得不等式组的解集为:-9<n≤-5,
∵n是整数
∴n为-8,-7,-6,-5,
∴当n=-5,方程的整数解为x=-5.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=10 cm,BC=6 cm,动点P从点C出发,以每秒2 cm的速度按C→A的路径运动,设运动时间为t秒.
(1)出发2秒时,△ABP的面积为 cm2;
(2)当t为何值时,BP恰好平分∠ABC?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,得
,得![]() ;
;![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,得
,得![]() ;……;
;……;![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,要使
,要使![]() 的度数为整数,则
的度数为整数,则![]() 的最大值为( )
的最大值为( )
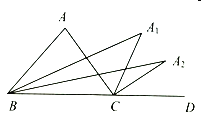
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:(1)b2﹣4ac>0;(2)abc>0;(3)8a+c>0;(4)6a+3b+c>0,其中正确的结论的个数是( )
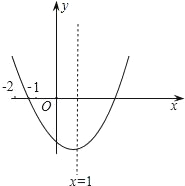
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣bx+2(﹣2≤b≤2),当b从﹣2逐渐增加到2的过程中,它所对应的抛物线的位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是( )
A. 先往左上方移动,再往左下方移动
B. 先往左下方移动,再往左上方移动
C. 先往右上方移动,再往右下方移动
D. 先往右下方移动,再往右上方移动
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
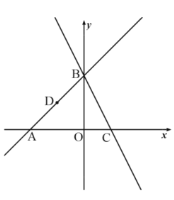
【题目】如图,![]() ,
,![]() 是直线
是直线![]() 与坐标轴的交点,直线
与坐标轴的交点,直线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() ,
,![]() 三点的坐标.
三点的坐标.
(2)当点![]() 是
是![]() 的中点时,在
的中点时,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的和最小,画出点
的和最小,画出点![]() 的位置,并求
的位置,并求![]() 点的坐标.
点的坐标.
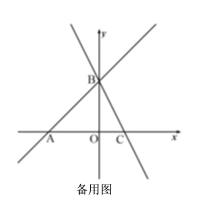
(3)若点![]() 是折线
是折线![]() 上一动点,是否存在点
上一动点,是否存在点![]() ,使
,使![]() 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com