
【题目】已知二次函数y=![]() (k是常数).
(k是常数).
(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=![]() 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;
(3)若抛物线y=![]() 与x轴交于A(
与x轴交于A(![]() ,0)、B(
,0)、B(![]() ,0)两点,且
,0)两点,且![]() <
<![]() ,
,![]() =34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于
=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )两点,试探究
)两点,试探究![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
【答案】(1) k<![]() ,且k≠0;(2) k<0;x<
,且k≠0;(2) k<0;x<![]() ;(3)1,理由详见解析.
;(3)1,理由详见解析.
【解析】
试题分析:(1)根据题意k≠0,△>0,列出不等式组即可解决问题.
(2)设反比例函数解析式为y=![]() ,因为经过点(1,k),所以m=k,再根据条件即可确定k的值以及x的范围.
,因为经过点(1,k),所以m=k,再根据条件即可确定k的值以及x的范围.
(3)结论:![]() =1.令y=0,则有
=1.令y=0,则有![]() =0,所以
=0,所以![]() +
+![]() =
=![]() ,
,![]() =
=![]() ,根据
,根据![]() =34,列出方程求出k的值,设过点P的直线为y=kx+3﹣k,由
=34,列出方程求出k的值,设过点P的直线为y=kx+3﹣k,由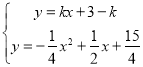 消去y得
消去y得![]() +(4k﹣2)x﹣3﹣4k=0,得
+(4k﹣2)x﹣3﹣4k=0,得![]() =﹣(4k﹣2),
=﹣(4k﹣2),![]() =﹣3﹣4k,根据
=﹣3﹣4k,根据![]() =
=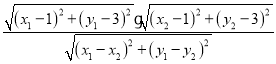 ,代入化简即可解决问题.
,代入化简即可解决问题.
试题解析:(1)∵二次函数y=![]() 与x轴有两个不同的交点,
与x轴有两个不同的交点,
∴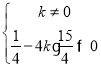 ,
,
解得k<![]() ,且k≠0.
,且k≠0.
所以若该函数的图象与x轴有两个不同的交点,k的取值范围是k<![]() ,且k≠0;
,且k≠0;
(2)设反比例函数解析式为y=![]() ,
,
∵经过点(1,k),
∴m=k,
∵反比例函数和二次函数y=![]() 都是y随x的增大而增大,
都是y随x的增大而增大,
∴k<0,x<![]() ,即x<
,即x<![]() .
.
(3)结论:![]() =1.
=1.
理由:令y=0,则有![]() =0,
=0,
∴![]() +
+![]() =
=![]() ,
,![]() =
=![]()
∵![]() =34,
=34,
∴![]() =34,
=34,
∴![]() =0,
=0,
解得k=![]() 或
或![]() ,
,
由(1)可知k<![]() ,
,
∴k=![]() ,
,
∴抛物线解析式为y=![]() ,
,
设过点P的直线为y=kx+b,把P(1,3)代入得3=k+b,
∴b=3﹣k,
∴过点P的直线为y=kx+3﹣k,
∵过点P的直线为y=kx+3﹣k与物线交于![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )两点,
)两点,
∴![]() =k
=k![]() +3﹣k,
+3﹣k,![]() =k
=k![]() +3﹣k,
+3﹣k,
由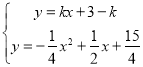 消去y得
消去y得![]() +(4k﹣2)x﹣3﹣4k=0,
+(4k﹣2)x﹣3﹣4k=0,
∴![]() =﹣(4k﹣2),
=﹣(4k﹣2),![]() =﹣3﹣4k ,
=﹣3﹣4k ,
∴![]() =
=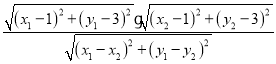 =
=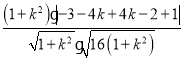 =1.
=1.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中x1 , x2 , x3分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),则有( ) 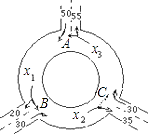
A.x1>x2>x3
B.x1>x3>x2
C.x2>x3>x1
D.x3>x2>x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球绕太阳转动一天通过的路程约是2640000千米,用科学记数法表示为( )
A.2.64×107
B.2.64×106
C.26.4×105
D.264×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=![]() x+3与两坐标轴分别相交于A、B两点,若点P、Q分别是线段AB、OB上的动点,且点P不与A、B重合,点Q不与O、B重合.
x+3与两坐标轴分别相交于A、B两点,若点P、Q分别是线段AB、OB上的动点,且点P不与A、B重合,点Q不与O、B重合.
(1)若OP⊥AB于点P,△OPQ为等腰三角形,这时满足条件的点Q有几个?请直接写出相应的OQ的长;
(2)当点P是AB的中点时,若△OPQ与△ABO相似,这时满足条件的点Q有几个?请分别求出相应的OQ的长;
(3)试探究是否存在以点P为直角顶点的Rt△OPQ?若存在,求出相应的OQ的范围,并求出OQ取最小值时点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽做一道数学题:“已知两个多项式A,B,B为 ![]() ﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是
﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是 ![]() +10x+12.根据以上信息,你能求出A+B的结果吗?
+10x+12.根据以上信息,你能求出A+B的结果吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
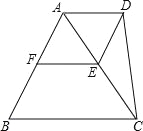
【题目】如图,点E、F分别是等边△ABC中AC、AB边上的中点,以AE为边向外作等边△ADE.
(1)求证:四边形AFED是菱形;
(2)连接DC,若BC=10,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式4x﹣4x3因式分解正确的是( )
A.﹣x(x+2)(x﹣2)B.x(x+2)(2﹣x)
C.﹣4x(x+1)(1﹣x)D.4x(x+1)(1﹣x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com