Question

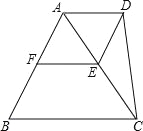
【题目】如图，点E、F分别是等边△ABC中AC、AB边上的中点，以AE为边向外作等边△ADE．

（1）求证：四边形AFED是菱形；

（2）连接DC，若BC=10，求四边形ABCD的面积．

Answer 1

【答案】(1)证明详见解析；(2)．

【解析】

试题分析：（1）由等边三角形的性质得出AF=EF=AE=DE=AD，由四边相等的四边形是菱形，即可得出结论；

（2）作AM⊥BC于M，由等边三角形的性质和三角函数求出AM，在求出AD的长，证出四边形ABCD是梯形，由梯形的面积公式即可得出结果．

试题解析：（1）∵△ABC、△ADE是等边三角形，

∴AF=EF=AE=DE=AD，∠ACB=∠DAE=60°，

∴四边形AFED是菱形；

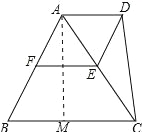
（2）解：作AM⊥BC于M，如图所示：

∵△ABC是等边三角形，

∴AC=BC=10，∠B=60°，

∴AM=ABsin60°=10×=，

∵E是AC的中点，

∴AE=AD=AC=5，

∵∠ACB=∠DAE=60°，

∴AD∥BC，

∴四边形ABCD是梯形，

∴四边形ABCD的面积=（AD+BC）×AM=（5+10）×=．