
【题目】在平面直角坐标系xOy中,对于P(a,b)和点Q(a,b′),给出如下定义:若b′= ,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5).
,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5).
(1)点(![]() ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;
(2)判断点A(﹣2,﹣1)、B(﹣1,2)中,哪一个点是函数y=![]() 图象上某一个点的限变点?并说明理由;
图象上某一个点的限变点?并说明理由;
(3)若点P(a,b)在函数y=﹣x+3的图象上,其限变点Q(a,b′)的纵坐标的取值范围是﹣6≤b′≤﹣3,求a的取值范围.
【答案】(1)(![]() ,1);(2)点A不是函数y=
,1);(2)点A不是函数y=![]() 图象上某一个点的限变点,点B函数y=
图象上某一个点的限变点,点B函数y=![]() 图象上某一个点的限变点.理由详见解析;(3) ﹣3≤a≤0或6≤a≤9.
图象上某一个点的限变点.理由详见解析;(3) ﹣3≤a≤0或6≤a≤9.
【解析】
试题分析:(1)根据限变点的定义即可直接求解;
(2)求得A和B的限变点,然后判断限变点是否在反比例函数的图象上即可;
(3)分成a≥1和a<1两种情况,然后根据﹣6≤b′≤﹣3,得到关于a的不等式,从而求得.
试题解析:(1)点(![]() ,1)的限变点的坐标是(
,1)的限变点的坐标是(![]() ,1).
,1).
故答案为:(![]() ,1);
,1);
(2)A(﹣2,﹣1)的限变点是(﹣2,1)、B(﹣1,2)的限变点是(﹣1,﹣2).
点(﹣2,1)不在函数y=![]() 上,则(﹣2,﹣1)不是y=
上,则(﹣2,﹣1)不是y=![]() 图象上某点的限变点;
图象上某点的限变点;
(﹣1,﹣2)在y=![]() 的图象上,则(﹣1,2)是y=
的图象上,则(﹣1,2)是y=![]() 图象上某点的限变点;
图象上某点的限变点;
(3)当a≥1时,b=﹣a+3,则﹣6≤﹣a+3≤﹣3,
解得:6≤a≤9;
当a<1时,b=a﹣3,则﹣6≤a﹣3≤﹣3,
解得:﹣3≤a≤0.
故a的范围是:﹣3≤a≤0或6≤a≤9.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】已知直线y=![]() x+3与两坐标轴分别相交于A、B两点,若点P、Q分别是线段AB、OB上的动点,且点P不与A、B重合,点Q不与O、B重合.
x+3与两坐标轴分别相交于A、B两点,若点P、Q分别是线段AB、OB上的动点,且点P不与A、B重合,点Q不与O、B重合.
(1)若OP⊥AB于点P,△OPQ为等腰三角形,这时满足条件的点Q有几个?请直接写出相应的OQ的长;
(2)当点P是AB的中点时,若△OPQ与△ABO相似,这时满足条件的点Q有几个?请分别求出相应的OQ的长;
(3)试探究是否存在以点P为直角顶点的Rt△OPQ?若存在,求出相应的OQ的范围,并求出OQ取最小值时点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
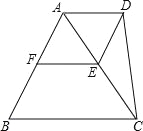
【题目】如图,点E、F分别是等边△ABC中AC、AB边上的中点,以AE为边向外作等边△ADE.
(1)求证:四边形AFED是菱形;
(2)连接DC,若BC=10,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年“一带一路”建设取得重大进展,据商务部数据显示,今年前11个月,我国与沿线国家贸易额达9831亿美元,这一数据用科学记数法可表示为_____美元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com