
����Ŀ����ֱ֪��y=![]() x+3����������ֱ��ཻ��A��B���㣬����P��Q�ֱ����߶�AB��OB�ϵĶ��㣬�ҵ�P����A��B�غϣ���Q����O��B�غϣ�
x+3����������ֱ��ཻ��A��B���㣬����P��Q�ֱ����߶�AB��OB�ϵĶ��㣬�ҵ�P����A��B�غϣ���Q����O��B�غϣ�
��1����OP��AB�ڵ�P����OPQΪ���������Σ���ʱ���������ĵ�Q�м�������ֱ��д����Ӧ��OQ�ij���
��2������P��AB���е�ʱ������OPQ����ABO���ƣ���ʱ���������ĵ�Q�м�������ֱ������Ӧ��OQ�ij���
��3����̽���Ƿ�����Ե�PΪֱ�Ƕ����Rt��OPQ�������ڣ������Ӧ��OQ�ķ�Χ�������OQȡ��Сֵʱ��P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡�(1) ��Q��������OQ�ij�Ϊ2��![]() ��
��![]() ��(2) 2����OQ�ij�Ϊ2��
��(2) 2����OQ�ij�Ϊ2��![]() ��(3)���ڣ�OQȡ��Сֵʱ��P�����꣨
��(3)���ڣ�OQȡ��Сֵʱ��P�����꣨![]() ��
��![]() ����
����
��������
�����������1����ͼ1�У����������ĵ�Q���������������������ۼ�����QO=QP����OP=OQ����PO=PQ��
��2����ͼ2�У����������ĵ�Q��2������![]() ��OB��
��OB��![]() ��
��![]() ��OP��
��OP��![]() ������֤��
������֤��![]() ��
��![]() �����������������������ε����ʼ��ɽ�����⣮
�����������������������ε����ʼ��ɽ�����⣮
��3�����ڣ���OQΪֱ������G������G��AB�����ڵ�Pʱ����OPQ=90�㣬��ʱOQ��ֵ��С���ɴ����OQ�����ɽ�����⣮
�����������1����ͼ1�У����������ĵ�Q��������
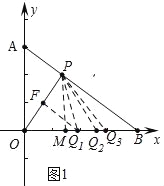
���ɣ���PM��OB��M����OP�Ĵ�ֱƽ���߽�OP��F����OB��![]() ����
����![]() =
=![]() ����
����![]() �ǵ��������Σ���ʱ
�ǵ��������Σ���ʱ![]() =
=![]() OB=2��
OB=2��
��A��0��3����B��4��0����
��OA=3��OB=4��AB=5��
��OP��AB��
��![]() OAOB=
OAOB=![]() ABOP��
ABOP��
��OP=![]() =
=![]() ��
��
��![]() =OPʱ����
=OPʱ����![]() �ǵ��������Σ���ʱ
�ǵ��������Σ���ʱ![]() =
=![]() ��
��
��PO=![]() ʱ����PM��
ʱ����PM��![]() ��
��
��![]() =2OM��
=2OM��
�ߡ�POM=��![]() ����PMO=��OPB��
����PMO=��OPB��
���OPM�ס�OBP��
��![]() =OMOB��
=OMOB��
��OM=![]() ��
��
��![]() =
=![]() .
.
������������OPQΪ����������ʱ�����������ĵ�Q��������OQ�ij�Ϊ2��![]() ��
��![]() ��
��
��2����ͼ2�У����������ĵ�Q��2����
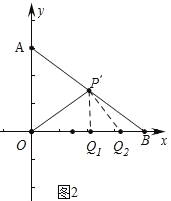
���ɣ���![]() ��OB��
��OB��![]() ��
��![]() ��OP��
��OP��![]() ��
��
��PA=PB����AOB=90�㣬
��PA=PB=PO��
���![]() =��ABO���ߡ�
=��ABO���ߡ�![]() =��AOB��
=��AOB��
���![]() �ס�BAO��
�ס�BAO��
��PA=PB��![]() ��OA��
��OA��
��![]() =
=![]() =
=![]() OB=2��
OB=2��
�ߡ�![]() =��ABO����
=��ABO����![]() =��AOB��
=��AOB��
���![]() �ס�BOA��
�ס�BOA��
��![]() ��
��
��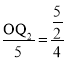 ��
��
��![]() =
=![]() ��
��
������������OPQ����ABO����ʱ�����������ĵ�Q��2����OQ�ij�Ϊ2��![]() ��
��
��3�����ڣ��������£�
��ͼ3�У���OQΪֱ������G������G��AB�����ڵ�Pʱ����OPQ=90�㣬��ʱOQ��ֵ��С��
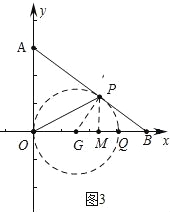
����OG=GP=r��
��AO=AP=3��
��PB=AB=AP=2��
��Rt��PBG�У��ߡ�GPB=90�㣬PG=r��BG=4��r��PB=2��
��![]() ��
��
��r=![]() ��
��
��OQ=2r=3��
����3��OQ��4ʱ����OPQ��Ϊֱ�������Σ�
��PM��OB��M��
��PM��OA��
��![]() ��
��
��![]() ��
��
��PM=![]() ��BM=
��BM=![]() ��
��
��OM=4��![]() =
=![]() ��
��
��OQȡ��Сֵʱ��P�����꣨![]() ��
��![]() ����
����


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
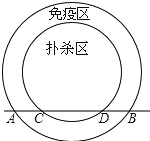
����Ŀ�����²����������DZ�SARS��Ⱦ�ٶȸ���Ĵ�Ⱦ����Ϊ��ֹ���������ӣ������涨�����ߵ�3km��Χ��Ϊ��ɱ�������ߵ�3km��5km��Χ��Ϊ������������ɱ�����������ڵĴ�ׯ����·ʵ��ȫ��չ���������һ����ֱ�Ĺ�·ABͨ�������в�������ͼ������ɱ���ڹ�·CD��Ϊ4km��
��1������ֱ�ߺ�Բ���ҳ��ߵ�O����д������������ͼ�ۼ�����
��2����������·�����������ж���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��[��x+2y����x��2y������x+4y��2]��4y������x=1��y=4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������һ��ƽ���ı��ε�ֽ�壬������ȷ��ֽ����״�Ƿ����С���ÿ̶ȳ���������ı��ε������߳���Ȼ�����С����ֽ���DZ���ƽ���ı��Σ�С��ó�������۵�������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
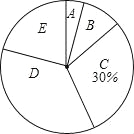
����Ŀ������5�·ݣ�ijУ���꼶ѧ���μ����������п��������ԣ�Ϊ���˽��У���꼶��1����ͬѧ���п������������ȫ��ѧ�����п������ɼ�������ͳ�ƣ����������²�������Ƶ���ֲ����������������ͳ��ͼ����ͼ��������ͼ���е���Ϣ����������⣺
��1����ȫ��ѧ��������m��ֵ��
��2��ֱ��д���ð�ѧ�����п������ɼ�����λ�������ĸ������Σ�
��3���ð��п������ɼ����ֹ���3�ˣ���������2�ˣ�Ů��1�ˣ��������3�������ѡȡ2�˵����꼶���о��齻�������á��б���������״ͼ�������ǡ��ѡ��һ��һŮ�ĸ��ʣ�
���� | �����Σ��֣� | Ƶ�� |
A | 36��x��41 | 2 |
B | 41��x��46 | 5 |
C | 46��x��51 | 15 |
D | 51��x��56 | m |
E | 56��x��61 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=![]() ��k�dz�������
��k�dz�������
��1�����ú�����ͼ����x����������ͬ�Ľ��㣬����k��ȡֵ��Χ��
��2�����㣨1��k����ij����������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ���y=![]() ����y��x�������������kӦ�����������x��ȡֵ��Χ��
����y��x�������������kӦ�����������x��ȡֵ��Χ��
��3����������y=![]() ��x�ύ��A��
��x�ύ��A��![]() ��0����B��
��0����B��![]() ��0�����㣬��
��0�����㣬��![]() ��
��![]() ��
��![]() =34������y�ƽ�е�ֱ��y=ax+b������P��1��3�������������߽���
=34������y�ƽ�е�ֱ��y=ax+b������P��1��3�������������߽���![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �����㣬��̽��
�����㣬��̽��![]() �Ƿ�Ϊ��ֵ����д��̽�����̣�
�Ƿ�Ϊ��ֵ����д��̽�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ε������ڽǵı���1:2:3����̱߳�Ϊ1cm����߳�Ϊ2cm������������������Ƕ����ֱ���______������һ�ߵ�ƽ����______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����P��a��b���͵�Q��a��b�䣩���������¶��壺��b��= ����Ƶ�QΪ��P���ޱ�㣮���磺�㣨2��3�����ޱ��������ǣ�2��3�����㣨��2��5�����ޱ��������ǣ���2����5����
����Ƶ�QΪ��P���ޱ�㣮���磺�㣨2��3�����ޱ��������ǣ�2��3�����㣨��2��5�����ޱ��������ǣ���2����5����
��1���㣨![]() ��1�����ޱ��������� ��
��1�����ޱ��������� ��
��2���жϵ�A����2����1����B����1��2���У���һ�����Ǻ���y=![]() ͼ����ijһ������ޱ�㣿��˵�����ɣ�
ͼ����ijһ������ޱ�㣿��˵�����ɣ�
��3������P��a��b���ں���y=��x+3��ͼ���ϣ����ޱ��Q��a��b�䣩���������ȡֵ��Χ�ǩ�6��b������3����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ�ѡ���У������������������ͬ���ǣ�������
A.a2a3B.��a2��3C.��a3��2D.a2a4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com