
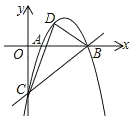
【题目】如图,抛物线经过A(1,0)、B(4,0)、C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连接DC、DB,则△BCD的面积的最大值是_____.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中
中![]() ,
,![]() 的三条角平分线交于点
的三条角平分线交于点![]() ,过
,过![]() 作
作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
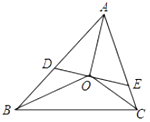
(1)写出图中的相似三角形(全等三角形除外),并选一对证明.
(2)若![]() ,
,![]() ,
,![]() 比
比![]() 长
长![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
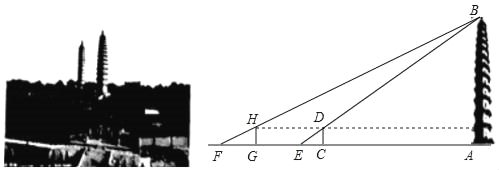
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(a﹣1)x2+3x﹣6的图象与x轴的交点为A和B,若点B一定在坐标原点和(1,0)之间,且B点不与原点和(1,0)重合,那么a的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
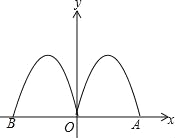
【题目】如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
A. 0<m<![]() B.
B. ![]() <m<
<m<![]()
C. 0<m<![]() D. m<
D. m<![]() 或m<
或m<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2.动点P以每秒2个单位长度的速度从点A出发,沿A→C→B的方向向终点B运动(点P不与△ABC的顶点重合).点P关于点C的对称点为点D,过点P作PQ⊥AB于点Q,以PD、PQ为边作□PDEQ.设□PDEQ与△ABC.重叠部分的面积为S,点P的运动时间为t(s)

(1)当点P在AC上运动时,用含t的代数式表示PD的长;
(2)当点E落在△ABC的直角边上时,求t的值;
(3)当□PDEQ与△ABC重叠部分的图形是四边形时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=![]() x与抛物线交于A、B两点,直线l为y=﹣1.
x与抛物线交于A、B两点,直线l为y=﹣1.
(1)求抛物线的解析式;
(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com