
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2.动点P以每秒2个单位长度的速度从点A出发,沿A→C→B的方向向终点B运动(点P不与△ABC的顶点重合).点P关于点C的对称点为点D,过点P作PQ⊥AB于点Q,以PD、PQ为边作□PDEQ.设□PDEQ与△ABC.重叠部分的面积为S,点P的运动时间为t(s)

(1)当点P在AC上运动时,用含t的代数式表示PD的长;
(2)当点E落在△ABC的直角边上时,求t的值;
(3)当□PDEQ与△ABC重叠部分的图形是四边形时,求S与t之间的函数关系式.
【答案】(1)4-4t;(2)![]() 或
或![]() ;(3)
;(3)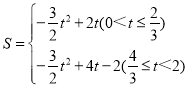
【解析】
(1)由题意得AP=2t,得到PC=2-2t,再根据对称性即可求解;
(2)根据题意作图分情况讨论,利用三角函数及三角形的关系即可列式求解;
(3)根据题意分情况讨论,利用割补法即可求解.
(1)∵AC=2,由题意得AP=2t,
∴PC=2-2t,
∵P、D关于C对称,
∴PD=2PC=4-4t;
(2)如图①,当P在BC边上时,PC=2t-2,∴PD=4t-4,
∵四边形PDEQ为平行四边形,
∴QE=PD=4t-4,QE∥PD,
∵∠ACB=90°,AC=BC=2,
∴∠A=∠B=45°,∠QEA=90°,
∴AQ=![]() =
=![]() (4t-4)
(4t-4)
∵BC=2,∴BP=4-2t,
∴QB=BP·cos45°=![]() (2-t)
(2-t)
∵AB=![]()
∴AQ+QB=![]() (4t-4)+
(4t-4)+![]() (2-t)=2
(2-t)=2![]()
解得t=![]() ;
;
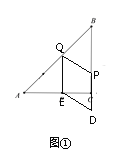
如图②,当P在AD边上时,由(1)得PD=4-4t,
∴QE=PD=4-4t,
∵∠B=45°,
QB=![]() (4-4t)
(4-4t)
∵AP=2t,
∴AQ=![]() t,
t,
∵AB=2![]()
∴![]() t+
t+![]() (4-4t)=2
(4-4t)=2![]()
解得t=![]() ;
;
综上,t=![]() 或
或![]() ;
;
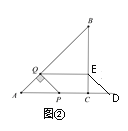
(3)如图③,由(2)得当![]() ,P在BC上时,设QE与AC交于M,
,P在BC上时,设QE与AC交于M,
∵PC=2t-2,
∴BP=2-(2t-2)=4-2t,
∴BQ=![]() (2-t)
(2-t)
∴AQ=AB-QB=2![]() -
-![]() (2-t)=
(2-t)=![]() t
t
∴AM=AQ·cos45°=t,
∴S△AMQ=![]() ,S△BQP=
,S△BQP=![]() BQ×QP=4-4t+
BQ×QP=4-4t+![]() ,
,
∴S四边形QMCP= S△ACB- S△AMQ- S△BQP=![]() ;
;
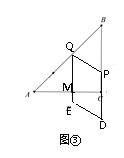
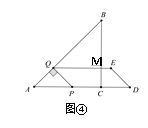
如图④,当![]() 时,P在AC上时,设QE与BC交于M,
时,P在AC上时,设QE与BC交于M,
∵AQ=![]() t
t
∴BQ=2![]() -
-![]() t
t
∴BM=BQ·cos45°=2-t,
∴S△QMB=![]() ,S△AQP=
,S△AQP=![]() ,
,
∴S四边形QMCP= S△ACB- S△QMB- S△AQP=![]()
综上,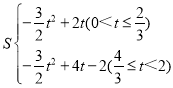 ,
,


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线经过点A(-3,0),点B(0,
中,直线经过点A(-3,0),点B(0,![]() ),点P的坐标为(1,0),与
),点P的坐标为(1,0),与![]() 轴相切于点O,若将⊙P沿
轴相切于点O,若将⊙P沿![]() 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
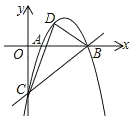
【题目】如图,抛物线经过A(1,0)、B(4,0)、C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连接DC、DB,则△BCD的面积的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元.每天可以销售
元.每天可以销售![]() 件,为尽快减少库存,商场决定降价促销.
件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件![]() 元,求两次下降的百分率;
元,求两次下降的百分率;
(2)经调查,若该商品每降价![]() 元,每天可多销售
元,每天可多销售![]() 件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?
件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
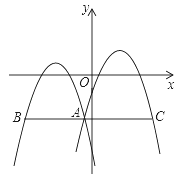
【题目】如图,在平面直角坐标系中,抛物线y=m(x+3)2+n与y=m(x﹣2)2+n+1交于点A.过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点C左侧),则线段BC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
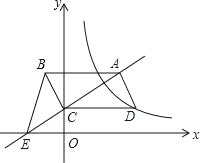
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数y=![]() (x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
(x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为13的菱形ABCD沿AD方向平移至DCEF的位置,作EG⊥AB,垂足为点G,GD的延长线交EF于点H,已知BD=24,则GH=_____.
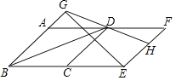
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(1)、九(2)两班的班长交流了为四川安雅地震灾区捐款的情况:
(Ⅰ)九(1)班班长说:“我们班捐款总数为1200元,我们班人数比你们班多8人.”
(Ⅱ)九(2)班班长说:“我们班捐款总数也为1200元,我们班人均捐款比你们班人均捐款多20%.”
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=4,E、F分别为AB、BC上的点,沿直线EF将∠B折叠,使点B恰好落在AC上的D处,当△ADE恰好为直角三角形时,BE的长为_____.
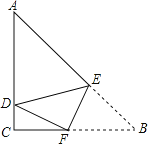
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com