
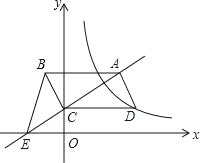
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数y=![]() (x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
(x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
【答案】4.
【解析】
过点D作DF⊥x轴于点F,设点D的坐标为(m,![]() )(m>0).由平行四边形的性质可得出BC=AD,再结合平行线的性质以及角的计算得出∠ECO=∠ADC,通过解直角三角形用∠ADC的余弦、m和k表示出BC和CE,由S△BCE=2结合三角形的面积公式即可得出关于k的一元一次方程,解方程即可得出结论;
)(m>0).由平行四边形的性质可得出BC=AD,再结合平行线的性质以及角的计算得出∠ECO=∠ADC,通过解直角三角形用∠ADC的余弦、m和k表示出BC和CE,由S△BCE=2结合三角形的面积公式即可得出关于k的一元一次方程,解方程即可得出结论;
解:过点D作DF⊥x轴于点F,如图所示.
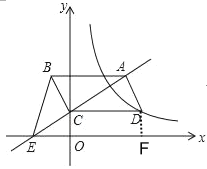
∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
又∵BC⊥AC,
∴DA⊥AC,
∵CD平行于x轴,
∴∠ACD=∠CEO.
∵CO⊥OE,DA⊥AC,
∴∠ECO=∠ADC,
设点D的坐标为(m,![]() )(m>0),
)(m>0),
则CD=m,OC=DF=![]() ,
,
在Rt△CAD中,CD=m,∠CAD=90°,AD=mcos∠ADC,
在Rt△COE中,OC=![]() ,∠COE=90°,CE=
,∠COE=90°,CE=![]() =
=![]() ,
,
∴S△BCE=![]() CEBC=
CEBC=![]() ·
·![]() mcos∠ADC=
mcos∠ADC=![]() k=2,
k=2,
解得:k=4,
故答案为:4.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示:
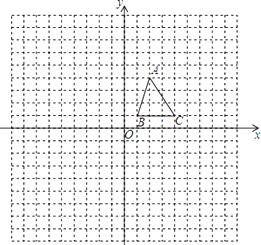
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在y轴左侧将△A1B1C1放大为原来的2倍,得到△A2B2C2,请画出△A2B2C2;
(3)设P(x,y)为△ABC内任意一点,△A2B2C2内的点P′是点P经过上述两次变换后的对应点,请直接写出P′的坐标___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(a﹣1)x2+3x﹣6的图象与x轴的交点为A和B,若点B一定在坐标原点和(1,0)之间,且B点不与原点和(1,0)重合,那么a的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠BCD=90°,ABCD=BCBD,BM∥CD交AD于点M.连接CM交DB于点N.
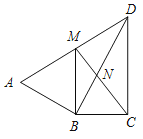
(1)求证:△ABD∽△BCD;
(2)若CD=6,AD=8,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2.动点P以每秒2个单位长度的速度从点A出发,沿A→C→B的方向向终点B运动(点P不与△ABC的顶点重合).点P关于点C的对称点为点D,过点P作PQ⊥AB于点Q,以PD、PQ为边作□PDEQ.设□PDEQ与△ABC.重叠部分的面积为S,点P的运动时间为t(s)

(1)当点P在AC上运动时,用含t的代数式表示PD的长;
(2)当点E落在△ABC的直角边上时,求t的值;
(3)当□PDEQ与△ABC重叠部分的图形是四边形时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
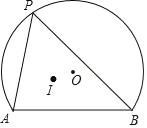
【题目】如图,AB为弓形AB的弦,AB=2![]() ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
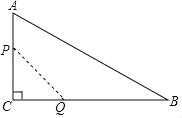
【题目】如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=24cm.动点P从点A开始沿边AC向点C以2cm/s的速度移动;动点Q从点C开始沿边CB向点B以4cm/s的速度移动.如果P,Q两点同时出发.
(1)经过几秒,△PCQ的面积为32cm2?
(2)若设△PCQ的面积为S,运动时间为t,请写出当t为何值时,S最大,并求出最大值;
(3)当t为何值时,以P,C,Q为顶点的三角形与△ABC相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com