
【题目】△ABC在平面直角坐标系中的位置如图所示:
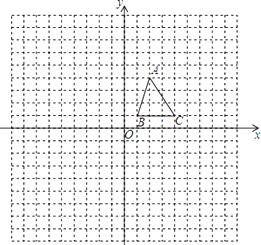
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在y轴左侧将△A1B1C1放大为原来的2倍,得到△A2B2C2,请画出△A2B2C2;
(3)设P(x,y)为△ABC内任意一点,△A2B2C2内的点P′是点P经过上述两次变换后的对应点,请直接写出P′的坐标___________.
【答案】(1)见解析;(2)见解析;(3) P′(-2x , 2y)
【解析】
(1)根据关于x轴对称性质找到A1、B1、C1的位置,然后画出图形即可;
(2)分别连接A1、B1、C1和O,然后反向延长扩大2倍,分别得到A2、B2、C2的位置,再画出图形即可;
(3)根据关于x轴对称的性质及位似特点写出P′坐标即可.
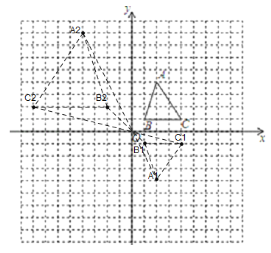
解:(1)根据关于x轴对称性质找到A1、B1、C1的位置,然后画出图形,如图△A1B1C1为所作;
(2)分别连接A1、B1、C1和O,然后反向延长扩大2倍,分别得到A2、B2、C2的位置,再画出图形,如图△A2B2C2为所作;
(3)根据关于x轴对称的性质得到变化坐标为(x,-y),以原点O为位似中心,在y轴左侧将△A1B1C1放大为原来的2倍得到P′的坐标为横纵坐标同时乘-2,即P′的坐标为(-2x,2y).


科目:初中数学 来源: 题型:
【题目】将一条长为![]() 的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
(1)要使这两个正方形的面积之和等于![]() ,那么这段铁丝剪成两段后的长度分别是多少?
,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于![]() 吗?若能,求出两段铁丝的长度;若不能,请说明理由。
吗?若能,求出两段铁丝的长度;若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
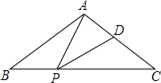
【题目】如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:△ABP∽△PCD;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
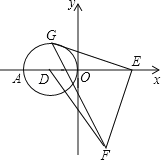
【题目】如图,平面直角坐标系中,点A(﹣4,0),点E (4,0),以AO为直径作⊙D,点G是⊙D上一动点,以EG为腰向下作等腰直角三角形EGF,连接DF,则DF的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线经过点A(-3,0),点B(0,
中,直线经过点A(-3,0),点B(0,![]() ),点P的坐标为(1,0),与
),点P的坐标为(1,0),与![]() 轴相切于点O,若将⊙P沿
轴相切于点O,若将⊙P沿![]() 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
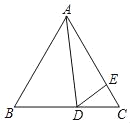
【题目】如图,等边△ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°
(1)求证:△ABD∽△DCE;
(2)若BD=4,CE=![]() ,求△ABC的边长.
,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
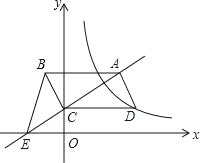
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数y=![]() (x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
(x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com