
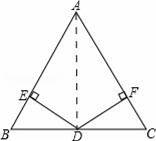
如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.
求证:DE=DF.


【考点】等腰三角形的性质;全等三角形的判定与性质.
【专题】证明题.
【分析】D是BC的中点,那么AD就是等腰三角形ABC底边上的中线,根据等腰三角形三线合一的特性,可知道AD也是∠BAC的角平分线,根据角平分线的点到角两边的距离相等,那么DE=DF.
【解答】证明:
证法一:连接AD.
∵AB=AC,点D是BC边上的中点
∴AD平分∠BAC(三线合一性质),
∵DE、DF分别垂直AB、AC于点E和F.
∴DE=DF(角平分线上的点到角两边的距离相等).
证法二:在△ABC中,
∵AB=AC
∴∠B=∠C(等边对等角) …
∵点D是BC边上的中点
∴BD=DC …
∵DE、DF分别垂直AB、AC于点E和F
∴∠BED=∠CFD=90°…
在△BED和△CFD中
∵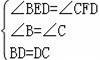
 ,
,
∴△BED≌△CFD(AAS),
∴DE=DF(全等三角形的对应边相等).

【点评】本题考查了等腰三角形的性质及全等三角形的判定与性质;利用等腰三角形三线合一的性质是解答本题的关键.


科目:初中数学 来源: 题型:
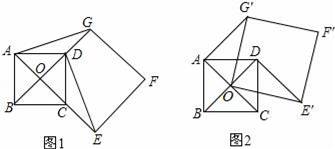
如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
| x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
| y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣11 | … |
由表格的数据判断b2﹣4ac 0(填>,<或=)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com