
 如图,在四边形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四边形ABCD.
如图,在四边形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四边形ABCD. 分析 先连接AC,在△ADC中利用勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ABC是直角三角形,再根据S四边形ABCD=S△ACD+S△ACB进行解答即可.
解答 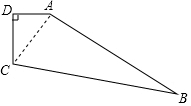 解:连接AC.
解:连接AC.
在△ADC中,
∵∠D=90°,
∴AC2=AD2+CD2(勾股定理).
由CD=3,AD=4,
得AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=5,
在△ABC中,
∵AB=12,BC=13,
∴BC2-AB2=132-122=25,
得:BC2=AB2+AC2,
∴∠CAB=90°(勾股定理的逆定理).
因此,S四边形ABCD=S△ACD+S△ACB
=$\frac{1}{2}$AD•DC+$\frac{1}{2}$AB•AC
=$\frac{1}{2}$×4×3+$\frac{1}{2}$×12×5
=6+30
=36.
点评 本题考查的是勾股定理及其逆定理,三角形的面积公式,根据勾股定理的逆定理判断出△ABC是直角三角形是解答此题的关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.88×102 | B. | 28.8×103 | C. | 2.88×104 | D. | 0.288×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
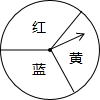 如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )
如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )| A. | 掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面 | |
| B. | 掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面 | |
| C. | 掷一枚质地均匀的骰子,奇数点朝上代表正面,偶数点朝上代表反面 | |
| D. | 转动如图所示的转盘,指针指向“红”代表正面,指针指向“蓝”代表反面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com