
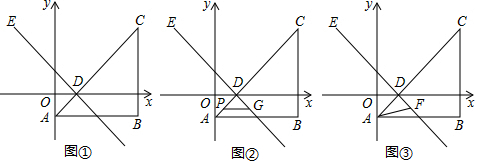
分析 (1)根据坐标的定义结合题意可得B、D、E的坐标,利用待定系数法即可求出直线DE的解析式.
(2)分两种情形①当$0≤t≤\sqrt{2}$时,PD=$\sqrt{2}$-t,可得S=$\frac{1}{2}$PD2=$\frac{1}{2}$($\sqrt{2}$-t)2=$\frac{1}{2}$t2-$\sqrt{2}$t+1.②当$\sqrt{2}<t≤4\sqrt{2}$时,同法可求.
(3)过点E作EK∥x轴交y轴于H,则∠KEF=∠EDO=45°.过点F作FG⊥EK于点G,则FG=EG=$\frac{\sqrt{2}}{2}$EF,由题意,动点M运动的路径为折线AF+EF,运动时间:t=AF+$\frac{\sqrt{2}}{2}$EF,推出t=AF+FG,即运动时间等于折线AF+FG的长度,由垂线段最短可知,折线AF+FG的长度的最小值为EK与线段AB之间的垂线段.则t最小=AH,直线DE与y轴的交点即为所求之F点.
解答 解:(1)如图①中,由题意得:B(4,-1),D(1,0).E(-2,3).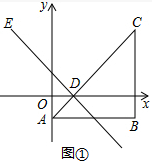
设直线DE为y=kx+b(k≠0)
把D(1,0).E(-2,3)代入得$\left\{{\begin{array}{l}{0=k+b}\\{3=-2k+b}\end{array}}\right.$
解之得:$\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$
∴直线DE为:y=-x+1.
(2)在Rt△ABC中,由BA=BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{2}$,
由AP=t (0≤t≤4$\sqrt{2}$),
同理可得:AD=$\sqrt{A{O}^{2}+O{D}^{2}}$=$\sqrt{2}$,
由题意可知:ED⊥AC,∠DPG=∠DAB=45°
∴△DPG为等腰直角三角形
S=$\frac{1}{2}$DP2,
如图②中,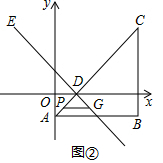
①当$0≤t≤\sqrt{2}$时,PD=$\sqrt{2}$-t,
∴S=$\frac{1}{2}$PD2=$\frac{1}{2}$($\sqrt{2}$-t)2=$\frac{1}{2}$t2-$\sqrt{2}$t+1.
②当$\sqrt{2}<t≤4\sqrt{2}$时,易得DP=t-$\sqrt{2}$,
∴S=$\frac{1}{2}$PD2=$\frac{1}{2}$(t-$\sqrt{2}$)2=$\frac{1}{2}$t2-$\sqrt{2}$t+1.
综上:S=$\frac{1}{2}$t2-$\sqrt{2}$t+1.(0≤t$≤4\sqrt{2}$)
(3)如图③,易得∠EDO=45°.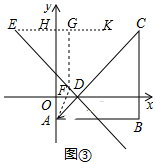
过点E作EK∥x轴交y轴于H,则∠KEF=∠EDO=45°.
过点F作FG⊥EK于点G,则FG=EG=$\frac{\sqrt{2}}{2}$EF,
由题意,动点M运动的路径为折线AF+EF,运动时间:t=AF+$\frac{\sqrt{2}}{2}$EF,
∴t=AF+FG,即运动时间等于折线AF+FG的长度,
由垂线段最短可知,折线AF+FG的长度的最小值为EK与线段AB之间的垂线段.
则t最小=AH,直线DE与y轴的交点即为所求之F点,
∵直线DE解析式为:y=-x+1
∴F(0,1),
综上所述,当点F(0,1)坐标为时,点M在整个运动过程中用时最少.
点评 本题考查一次函数综合题、等腰直角三角形的性质、待定系数法、三角形的面积、垂线段最短等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考压轴题.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:选择题
| A. | -|-2|=2 | B. | (6.4×106)÷(8×103)=800 | ||
| C. | (-1)2015-12016=-2 | D. | $-6÷({\frac{1}{3}-\frac{1}{2}})=36$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
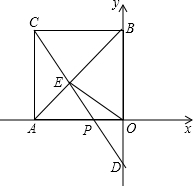 在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D.
在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度.
为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com