
【题目】直线l1交x轴于点A(6![]() ,0),交y轴于B(0,6).
,0),交y轴于B(0,6).
(1)如图,折叠△AOB,使BA落在y轴上,折痕所在直线为l2,直线l2与x轴交与C点,求C点坐标及l2的解析式;
(2)在直线l1上找点M,使得以M、A、C为顶点的三角形是等腰三角形,求出所有满足条件的M点的坐标.

【答案】(1)C(2![]() ,0),y=﹣
,0),y=﹣![]() x+6;(2)点M(6
x+6;(2)点M(6![]() ﹣6,2
﹣6,2![]() )或(6
)或(6![]() +6,﹣2
+6,﹣2![]() )或(4
)或(4![]() ,2)或(0,6).
,2)或(0,6).
【解析】
(1)由三角函数可求∠OAB=30°,由折叠的性质和直角三角形的性质可求点C坐标,用待定系数法可求解析式;
(2)分三种情况讨论,由等腰三角形的性质可求解.
解:∵点A(6![]() ,0),交y轴于B(0,6).
,0),交y轴于B(0,6).
∴OA=6![]() ,OB=6,
,OB=6,
∴tan∠OAB=![]() ,
,
∴∠OAB=30°,
∴∠OBA=60°,
∵折叠△AOB,
∴∠OBC=∠ABC=30°,
∴BC=2OC,BO=![]() OC=6,
OC=6,
∴OC=2![]() ,
,
∴点C(2![]() ,0),
,0),
设直线BC解析式为:y=kx+b,

解得:
∴直线BC解析式为:y=﹣![]() x+6;
x+6;
(2)当点M与点B重合时,
由(1)可知:∠AMC=∠MAC=30°,
∴CM=AC,
∴△ACM是等腰三角形,
∴当M为(0,6)时,△ACM是等腰三角形,
∵OC=2![]() ,OA=6
,OA=6![]() ,
,
∴AC=4![]() ,
,
若AM=AC=4![]() ,
,
如图1:过点M作MH⊥AC,

∵∠MAH=30°,
∴MH=![]() AM=2
AM=2![]() ,AH=2
,AH=2![]() MH=6,
MH=6,
∴OH=6![]() ﹣6或6
﹣6或6![]() +6,
+6,
∴点M(6![]() ﹣6,2
﹣6,2![]() )或(6
)或(6![]() +6,﹣2
+6,﹣2![]() )
)
若AM=MC,
如图2,过点M作MH⊥AC,

∵AM=MC,MH⊥AC,
∴AH=CH=2![]() ,
,
∴OC=4![]() ,
,
∵∠MAH=30°,
∴AH=![]() MH,
MH,
∴MH=2,
∴点M(4![]() ,2),
,2),
综上所述:点M(6![]() ﹣6,2
﹣6,2![]() )或(6
)或(6![]() +6,﹣2
+6,﹣2![]() )或(4
)或(4![]() ,2)或(0,6).
,2)或(0,6).


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0),B(3,0),探究:抛物线![]() (m为常数)交x轴于点M、N两点.
(m为常数)交x轴于点M、N两点.
(1)当m=2时.
①求出抛物线的顶点坐标及线段MN的长;
②抛物线上有一点P,使![]() ,求出点P的坐标;
,求出点P的坐标;
(2)对于抛物线![]() (m为常数).
(m为常数).
①线段MN的长是否发生变化,请说明理由.
②若该抛物线与线段AB有公共点,请直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+8与x轴,y轴分别交于点A,B,直线y=x+1与直线AB交于点C,与y轴交于点D.
x+8与x轴,y轴分别交于点A,B,直线y=x+1与直线AB交于点C,与y轴交于点D.

(1)求点C的坐标.
(2)求△BDC的面积.
(3)如图,P是y轴正半轴上的一点,Q是直线AB上的一点,连接PQ.

①若PQ∥x轴,且点A关于直线PQ的对称点A′恰好落在直线CD上,求PQ的长.
②若△BDC与△BPQ全等(点Q不与点C重合),请写出所有满足要求的点Q坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=![]() (x<0)的图象与直线y=
(x<0)的图象与直线y=![]() x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=﹣
x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=﹣![]() ,xA﹣xB=﹣3,则k的值是( )
,xA﹣xB=﹣3,则k的值是( )

A. ﹣5 B. ![]() C. ﹣2 D. ﹣1
C. ﹣2 D. ﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
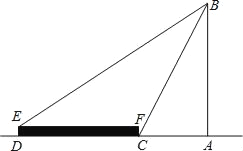
【题目】如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com