
【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD 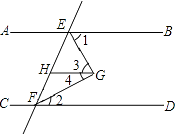
求证:∠EGF=90°
①把下列证明过程及理由补充完整.
②请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ()
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+=180° ()
又∵EG平分∠BEF(已知)
∴∠1= ![]() ∠
∠
又∵FG平分∠EFD(已知)
∴∠2= ![]() ∠EFD (同理)
∠EFD (同理)
∴∠1+∠2= ![]() (+)
(+)
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°.
【答案】两直线平行,内错角相等;EFD;两直线平行,同旁内角互补;BEF;∠BEF;∠EFD
【解析】证明:∵HG∥AB(已知),
∴∠1=∠3,
又∵HG∥CD(已知),
∴∠2=∠4(两直线平行,内错角相等),
∵AB∥CD(已知),
∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补),
又∵EG平分∠BEF(已知),
∴∠1= ![]() ∠BEF(角平分线的定义),
∠BEF(角平分线的定义),
又∵FG平分∠EFD(已知),
∴∠2= ![]() ∠EFD(角平分线的定义),
∠EFD(角平分线的定义),
∴∠1+∠2= ![]() (∠BEF+∠EFD),
(∠BEF+∠EFD),
∴∠1+∠2=90°,
∴∠3+∠4=90°(等量代换)
即∠EGF=90°.
所以答案是:两直线平行,内错角相等,∠EFD,两直线平行,同旁内角互补,角平分线的定义,EFD,∠BEF.两直线平行,内错角相等;
∠EFD; 两直线平行,同旁内角互补;
∠BEF;角平分线的定义;
∠BEF;∠EFD;
两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.
【考点精析】关于本题考查的平行线的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市质检部门对该市某超市沐浴露的质量进行抽样调查,其中A品牌的沐浴露有400瓶、B品牌的沐浴露有360瓶、C品牌的沐浴露有500瓶,考虑到不同品牌的质量差异,为保证样本有较好的代表性,该质检部门按5%的比例抽样,A品牌应调查________瓶,B品牌应调查________瓶,C品牌应调查________瓶.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于方程x2+2x﹣4=0的根的情况,下列结论错误的是( )
A. 有两个不相等的实数根B. 两实数根的和为﹣2
C. 没有实数根D. 两实数根的积为﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形如果是轴对称图形,那么它的边数与对称轴的条数之间存在联系吗?
(1)以凸六边形为例,如果这个凸六边形是轴对称图形,那么它可能有条对称轴;
(2)凸五边形可以恰好有两条对称轴吗?如果存在请画出图形,并用虚线标出两条对称轴;否则,请说明理由;
(3)通过对(1)中凸六边形的研究,请大胆猜想,一个凸多边形如果是轴对称图形,那么它的边数与对称轴的条数之间的联系是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为()
A.(﹣8,﹣2)
B.(﹣2,﹣2)
C.(2,4)
D.(﹣6,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种生物孢子的直径为0.000 63m,用科学记数法表示为( )
A.0.63×10﹣3m
B.6.3×10﹣4m
C.6.3×10﹣3m
D.6.3×10﹣5m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com