
【题目】一个多边形如果是轴对称图形,那么它的边数与对称轴的条数之间存在联系吗?
(1)以凸六边形为例,如果这个凸六边形是轴对称图形,那么它可能有条对称轴;
(2)凸五边形可以恰好有两条对称轴吗?如果存在请画出图形,并用虚线标出两条对称轴;否则,请说明理由;
(3)通过对(1)中凸六边形的研究,请大胆猜想,一个凸多边形如果是轴对称图形,那么它的边数与对称轴的条数之间的联系是: .
【答案】
(1)1,2,3或6
(2)
解:不可以.
理由如下:
根据轴对称图形的定义,若一个凸多边形是轴对称图形,则对称轴与多边形的交点是多边形的顶点或一条边的中点.若多边形的边数是奇数,则对称轴必经过一个顶点和一条边的中点.
如图1,设凸五边形ABCDE是轴对称图形,恰好有两条对称轴l1,l2,其中l1经过A和CD的中点.
若l2⊥l1,则l2与五边形ABCDE的两个交点关于l1对称,与对称轴必经过一个顶点和一条边的中点矛盾;
若l2不垂直于l1,则l2关于l1的对称直线也是五边形ABCDE的对称轴,与恰好有两条对称轴矛盾.
所以,凸五边形不可以恰好有两条对称轴
(3)对称轴的条数是多边形边数的约数
【解析】解:(1)凸六边形是轴对称图形,那么它可能有1,2,3或6条对称轴,
故答案为:1,2,3或6;(3)对称轴的条数是多边形边数的约数.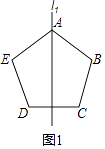
(1)根据凸六边形进行画图,然后猜想即可;(2)根据题意画出图形,再结合轴对称图形的定义进行分析即可;(3)根据(1)中所得的数据可得答案.


科目:初中数学 来源: 题型:
【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2=(),
又因为∠1=∠2,
所以∠1=∠3(),
所以AB∥(),
所以∠BAC+=180°(),
因为∠BAC=80°,
所以∠AGD= . 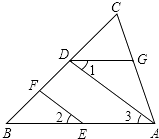
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题: 老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下: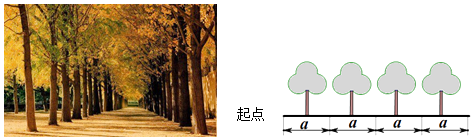
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
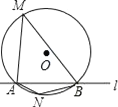
【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为16cm,AC与BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( ) 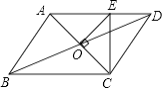
A.4cm
B.6cm
C.8cm
D.10cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com