
【题目】如果一个数的平方根是a+6和2a﹣15,则这个数为 .
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路: 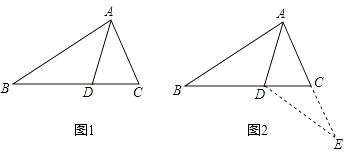
如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.
(1)判定△ABD与△AED全等的依据是;
(2)∠ACB与∠ABC的数量关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.
求:(1)tanC;
(2)图中两部分阴影面积的和.
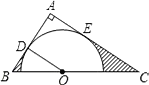
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD 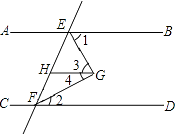
求证:∠EGF=90°
①把下列证明过程及理由补充完整.
②请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ()
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+=180° ()
又∵EG平分∠BEF(已知)
∴∠1= ![]() ∠
∠
又∵FG平分∠EFD(已知)
∴∠2= ![]() ∠EFD (同理)
∠EFD (同理)
∴∠1+∠2= ![]() (+)
(+)
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B左侧),其顶点为P,直线y=kx+b过抛物线与x轴的一个交点A,且与抛物线相交的另外一个交点为C,若S△ABC=10,请你回答下列问题:
(1)求直线的解析式;
(2)求四边形APBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(ax2﹣2xy+y2)﹣(﹣ax2+bxy+2y2)=6x2﹣9xy+cy2成立,则a,b,c的值分别为( )
A. 3,﹣7,﹣1 B. ﹣3,7,﹣1 C. 3,7,﹣1 D. ﹣3,﹣7,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题: 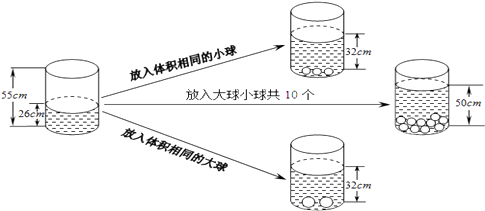
(1)放入一个小球水面升高cm,放入一个大球水面升高cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级350名学生的视力情况,从中抽查了80名学生的视力.在这个问题中,总体、个体、样本各是什么?上述问题采用的调查方式是普查还是抽样调查?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com