
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( ) 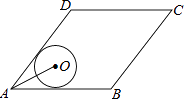
A.5
B.6
C.2 ![]()
D.3 ![]()
【答案】C
【解析】解:如图作DH⊥AB于H,连接BD,延长AO交BD于E. 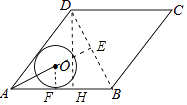
∵菱形ABCD的边AB=20,面积为320,
∴ABDH=32O,
∴DH=16,
在Rt△ADH中,AH= ![]() =12,
=12,
∴HB=AB﹣AH=8,
在Rt△BDH中,BD= ![]() =8
=8 ![]() ,
,
设⊙O与AB相切于F,连接AF.
∵AD=AB,OA平分∠DAB,
∴AE⊥BD,
∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,
∴△AOF∽△DBH,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴OF=2 ![]() .
.
故选C.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】某文具店5月份购进一批A种毕业纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请求出y与x的函数关系式;
(2)该文具店计划6月份新进一批A、B两种纪念册共100本,且B种纪念册的进货数量不超过A种纪念册的2倍,应如何进货才能使这批纪念册获利最多?A、B两种型号纪念册的进货和销售价格如下表:
A种 | B种 | |
进货价格(元/本) | 20 | 24 |
销售价格(元/本) | 25 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图所示,已知点C在线段AB上,线段AB=12,点M,N分别是AC,BC的中点,求线段MN的长度.
(2)把(1)中的“点C在线段AB上”改为“点C在线段AB延长上”,其他条件均不变,画图并求出线段MN的长度;
(3)已知线段AB,点C为直线AB外任意一点,点M,N分别是AC,BC的中点,连接MN,画图并猜想线段MN与线段AB的数量关系.(只要求画图,写出结论)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
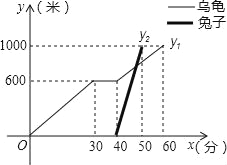
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟免再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程),有下列说法:
①兔子和乌龟同时从起点出发;②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟; ④兔子比乌龟早10分钟到达终点.
其中正确的说法是_____(把你认为正确说法的序号都填上);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P是△ABC的边AC上一点.
(1)写出点A、C的坐标:A: ;C:
(2)△ABC的面积为
(3)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称.
(4)若点P的坐标为(a+1,b﹣1),点P关于y轴的对称点为点Q,则点Q的坐标为 (用含字母a或b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) (﹣2x)3﹣(﹣x)·(3x)2
(2) (2a+b)(4a2+b2)(2a﹣b)
(3)(π﹣3.14)0+(﹣1)3+(![]() )-3÷(﹣2)
)-3÷(﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com