
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
【答案】
(1)
如图1中,
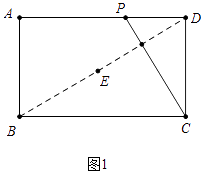
∵四边形ABCD是矩形,
∴∠ADC=∠A=90°,
∴∠DCP+∠CPD=90°,
∵∠CPD+∠ADB=90°,
∴∠ADB=∠PCD,
∵∠A=∠CDP=90°,
∴△ABD∽△DPC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PD= ![]() ,
,
∴t= ![]() s时,B、E、D共线.
s时,B、E、D共线.
(2)
如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
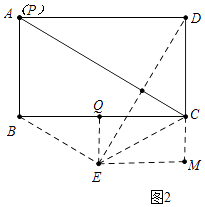
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90°,
∴EM= ![]() =
= ![]() =
= ![]() ,
,
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AD=4 ![]() ,
,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
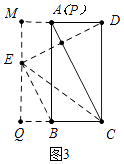
在Rt△ECQ中,QC=DM= ![]() =
= ![]() ,
,
由△DME∽△CDA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AD= ![]() ,
,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围 ![]() ≤m<4
≤m<4 ![]() .
.
【解析】(1)只要证明△ABD∽△DPC,可得 ![]() =
= ![]() ,由此求出PD即可解决问题;(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3;
,由此求出PD即可解决问题;(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】观察等式:① ![]() =1﹣
=1﹣ ![]() ;②
;② ![]() =
= ![]() ﹣
﹣ ![]() ;③
;③ ![]() =
= ![]() ﹣
﹣ ![]() ;④
;④ ![]() =
= ![]() ﹣
﹣ ![]() ,…
,…
(1)试用字母n的等式表示出你发现的规律,并证明该等式成立;
(2)![]()
+ ![]() +
+ ![]() +…+
+…+ ![]() = . (直接写出结果)
= . (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( ) 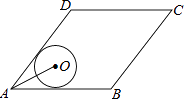
A.5
B.6
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人玩扑克牌游戏,他们先取出两张红心和两张黑桃共四张扑克牌,洗匀后背面朝上放在桌面上,每人抽取其中一张,拿到相同颜色的即为游戏搭档,现甲、乙两人各抽取了一张,求两人恰好成为游戏搭档的概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1,![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com