
【题目】如图,在平面直角坐标系中,点P是△ABC的边AC上一点.
(1)写出点A、C的坐标:A: ;C:
(2)△ABC的面积为
(3)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称.
(4)若点P的坐标为(a+1,b﹣1),点P关于y轴的对称点为点Q,则点Q的坐标为 (用含字母a或b的代数式表示)

【答案】(1)A(﹣3,4),B(﹣4,2);(2)25;(3)详见解析;(4)(﹣a﹣1,b﹣1).
【解析】
(1)直接利用平面直角坐标系得出各点坐标即可;
(2)利用△ABC所在矩形面积减去周围多余三角形的面积进而得出答案;
(3)利用关于y轴对称点的性质得出对应点坐标即可;
(4)利用关于y轴对称点的性质得出对应点坐标即可.
(1)如图所示:

A(﹣3,4),B(﹣4,2);
故答案为:(﹣3,4),(﹣4,2);
(2)△ABC的面积为:2×3﹣![]() ×1×2﹣
×1×2﹣![]() ×1×3﹣
×1×3﹣![]() ×1×2=2.5;
×1×2=2.5;
故答案为:2.5;
(3)如图所示:△A1B1C1,即为所求;
(4)点P的坐标为(a+1,b﹣1),点P关于y轴的对称点为点Q,则点Q的坐标为:(﹣a﹣1,b﹣1).
故答案为:(﹣a﹣1,b﹣1).


科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,4),B(2,0).
(1)求直线AB的函数解析式;
(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x﹣m)2+n与线段OA交于点C.
①求线段AC的长;(用含m的式子表示)
②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= ![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C. 
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)结合图象直接写出不等式kx+b< ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( ) 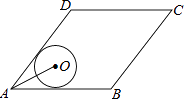
A.5
B.6
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2 , 一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由 ![]() ,EF,
,EF, ![]() ,AB所围成图形(图中阴影部分)的面积等于 .
,AB所围成图形(图中阴影部分)的面积等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人玩扑克牌游戏,他们先取出两张红心和两张黑桃共四张扑克牌,洗匀后背面朝上放在桌面上,每人抽取其中一张,拿到相同颜色的即为游戏搭档,现甲、乙两人各抽取了一张,求两人恰好成为游戏搭档的概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com