
【题目】如图,已知点A(0,4),B(2,0).
(1)求直线AB的函数解析式;
(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x﹣m)2+n与线段OA交于点C.
①求线段AC的长;(用含m的式子表示)
②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.
【答案】
(1)
解:设直线AB的函数解析式为:y=kx+b.
∵点A坐标为(0,4),点B坐标为(2,0),
∴ ![]() ,解得:
,解得: ![]() ,
,
即直线AB的函数解析式为y=﹣2x+4
(2)
解:①∵以M为顶点的抛物线为y=(x﹣m)2+n,
∴抛物线顶点M的坐标为(m,n).
∵点M在线段AB上,∴n=﹣2m+4,
∴y=(x﹣m)2﹣2m+4.
把x=0代入y=(x﹣m)2﹣2m+4,
得y=m2﹣2m+4,即C点坐标为(0,m2﹣2m+4),
∴AC=OA﹣OC=4﹣(m2﹣2m+4)=﹣m2+2m;
②存在某一时刻,能够使得△ACM与△AMO相似.理由如下:
过点M作MD⊥y轴于点D,则D点坐标为(0,﹣2m+4),
∴AD=OA﹣OD=4﹣(﹣2m+4)=2m.
∵M不与点A、B重合,∴0<m<2,
又∵MD=m,∴AM= ![]() =
= ![]() m.
m.
∵在△ACM与△AMO中,∠CAM=∠MAO,∠MCA>∠AOM,
∴当△ACM与△AMO相似时,假设△ACM∽△AMO,
∴ ![]() ,即
,即 ![]() ,
,
整理,得 9m2﹣8m=0,解得m= ![]() 或m=0(舍去),
或m=0(舍去),
∴存在一时刻使得△ACM与△AMO相似,且此时m= ![]() .
.

【解析】(1)设直线AB的函数解析式为:y=kx+b,将A、B两点的坐标代入,运用待定系数法即可求出直线AB的函数解析式;(2)①先由抛物线的顶点式为y=(x﹣m)2+n得出顶点M的坐标为(m,n),由点M是线段AB上一动点,得出n=﹣2m+4,则y=(x﹣m)2﹣2m+4,再求出抛物线y=(x﹣m)2+n与y轴交点C的坐标,然后根据AC=OA﹣OC即可求解;②过点M作MD⊥y轴于点D,则D点坐标为(0,﹣2m+4),AD=OA﹣OD=2m,由勾股定理求出AM= ![]() m.在△ACM与△AMO中,由于∠CAM=∠MAO,∠MCA>∠AOM,所以当△ACM与△AMO相似时,只能是△ACM∽△AMO,根据相似三角形对应边成比例得出
m.在△ACM与△AMO中,由于∠CAM=∠MAO,∠MCA>∠AOM,所以当△ACM与△AMO相似时,只能是△ACM∽△AMO,根据相似三角形对应边成比例得出 ![]() ,即
,即 ![]() ,解方程求出m的值即可.
,解方程求出m的值即可.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E . 若∠A=60°,BC=6,则图中阴影部分的面积为
A.![]() π
π
B.![]() π
π
C.![]() π
π
D.3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店5月份购进一批A种毕业纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请求出y与x的函数关系式;
(2)该文具店计划6月份新进一批A、B两种纪念册共100本,且B种纪念册的进货数量不超过A种纪念册的2倍,应如何进货才能使这批纪念册获利最多?A、B两种型号纪念册的进货和销售价格如下表:
A种 | B种 | |
进货价格(元/本) | 20 | 24 |
销售价格(元/本) | 25 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明平时喜欢玩“QQ农场”游戏,本学期初二年级数学备课组组织了几次数学反馈性测试,小明的数学成绩如下表:
月份x(月) | 9 | 10 | 11 | 12 | … |
成绩y(分) | 90 | 80 | 70 | 60 | … |
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在下列直角坐标系中描点;

(2)观察①中所描点的位置关系,照这样的发展趋势,猜想y与x之间的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“QQ农场”游戏,照这样的发展趋势,请你估计元月份的期末考试中小明的数学成绩,并用一句话对小明提出一些建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为6,M、N分别是边BC、CD上的点,且MC=2MB,ND=2NC,点P是对角线BD上一点,则PM+PN的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G. 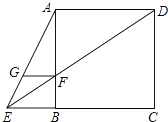
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P是△ABC的边AC上一点.
(1)写出点A、C的坐标:A: ;C:
(2)△ABC的面积为
(3)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称.
(4)若点P的坐标为(a+1,b﹣1),点P关于y轴的对称点为点Q,则点Q的坐标为 (用含字母a或b的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com