练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在直线AB上任取一点O，过点O作射线OC,OD，使当时，的度数是（ ）

    A. B. C. 或 D. 或

    【答案】D

    【解析】

    分射线OC、OD在直线AB的两侧两种情况作出图形，在同一侧时，根据平角等于180°列式计算即可得解，在两侧时，先求出∠AOD，再根据邻补角的定义列式计算即可得解．

    如图，

    射线OC、OD在直线AB的同一侧时，

    ∵∠COD=90°，

    ∴∠BOD=180°-90°-∠AOC=180°-90°-40°=50°，

    射线OC、OD在直线AB的两侧时，

    ∵∠COD=90°，

    ∴∠AOD=90°-∠AOC=90°-40°=50°，

    ∴∠BOD=180°-∠AOD=180°-50°=130°，

    综上所述，∠BOD的度数50°或130°．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算下列各题

    （1）

    （2）（2x）2x4÷x

    （3）

    （4）

    （5）（x﹣2）（2+x）﹣（2﹣x）（x﹣2）

    （6）（6x4y2+8x3y4）÷2xy2﹣（﹣2xy）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察等式：① =1﹣ ；② = ﹣ ；③ = ﹣ ；④ = ﹣ ，…
    （1）试用字母n的等式表示出你发现的规律，并证明该等式成立；
    （2）
    + + +…+ = ． （直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】反比例函数y= （a＞0，a为常数）和y= 在第一象限内的图象如图所示，点M在y= 的图象上，MC⊥x轴于点C，交y= 的图象于点A；MD⊥y轴于点D，交y= 的图象于点B，当点M在y= 的图象上运动时，以下结论：①S△ODB=S△OCA；②四边形OAMB的面积不变；③当点A是MC的中点时，则点B是MD的中点．其中正确结论的序号是 ．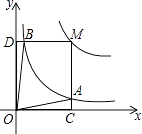

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A（n，﹣2），B（1，4）是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点，直线AB与y轴交于点C．
    （1）求反比例函数和一次函数的关系式；
    （2）求△AOC的面积；
    （3）结合图象直接写出不等式kx+b＜ 的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“书香包河”读书活动中，学校准备购买一批课外读物，为使课外读物满足学生们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图．请你根据统计图提供的信息，解答下列问题：

    (1)本次调查中，一共调查了______________名同学；

    (2)条形统计图中，m=_________，n=__________；

    (3)扇形统计图中，艺术类读物所在扇形的圆心角是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的边AB=20，面积为320，∠BAD＜90°，⊙O与边AB，AD都相切，AO=10，则⊙O的半径长等于（ ）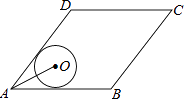
    A.5
    B.6
    C.2
    D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙、丁四人玩扑克牌游戏，他们先取出两张红心和两张黑桃共四张扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色的即为游戏搭档，现甲、乙两人各抽取了一张，求两人恰好成为游戏搭档的概率．（请用“画树状图”或“列表”等方法写出分析过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的反称点的定义如下：若在射线CP上存在一点P′，满足CP+CP′=2r，则称P′为点P关于⊙C的反称点，如图为点P及其关于⊙C的反称点P′的示意图．
    特别地，当点P′与圆心C重合时，规定CP′=0

    （1）当⊙O的半径为1时．
    ①分别判断点M（2，1），N（，0），T（1，）关于⊙O的反称点是否存在？若存在，求其坐标；
    ②点P在直线y=﹣x+2上，若点P关于⊙O的反称点P′存在，且点P′不在x轴上，求点P的横坐标的取值范围；
    （2）⊙C的圆心在x轴上，半径为1，直线y=﹣x+2与x轴、y轴分别交于点A，B，若线段AB上存在点P，使得点P关于⊙C的反称点P′在⊙C的内部，求圆心C的横坐标的取值范围．

    查看答案和解析>>

    同步练习册答案