
【题目】反比例函数y= ![]() (a>0,a为常数)和y=
(a>0,a为常数)和y= ![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y= ![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y= ![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y= ![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y= ![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 .
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 . 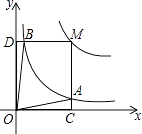
【答案】①②③
【解析】解:解:①由于A、B在同一反比例函数y= ![]() 图象上,则△ODB与△OCA的面积相等,都为
图象上,则△ODB与△OCA的面积相等,都为 ![]() ×2=1,正确; ②由于矩形OCMD、三角形ODB、三角形OCA为定值,则四边形MAOB的面积不会发生变化,正确;
×2=1,正确; ②由于矩形OCMD、三角形ODB、三角形OCA为定值,则四边形MAOB的面积不会发生变化,正确;
③连接OM,点A是MC的中点,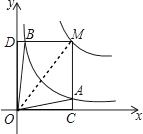
则△OAM和△OAC的面积相等,
∵△ODM的面积=△OCM的面积= ![]() ,△ODB与△OCA的面积相等,
,△ODB与△OCA的面积相等,
∴△OBM与△OAM的面积相等,
∴△OBD和△OBM面积相等,
∴点B一定是MD的中点.正确
故答案是:①②③.
【考点精析】利用反比例函数的图象和比例系数k的几何意义对题目进行判断即可得到答案,需要熟知反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


科目:初中数学 来源: 题型:
【题目】下列命题为真命题的是
A.有两边及一角对应相等的两个三角形全等
B.方程x2+2x+3=0有两个不相等的实数根
C.面积之比为1∶2的两个相似三角形的周长之比是1∶4
D.顺次连接任意四边形各边中点得到的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为6,M、N分别是边BC、CD上的点,且MC=2MB,ND=2NC,点P是对角线BD上一点,则PM+PN的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且交边CD于点E. 
(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2,若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】应用探究题 在图①中,已知长方形的长和宽分别为a,b,将线段A1A2向右平移1个单位长度到B1B2的位置,得到封闭图形A1A2B2B1(即阴影部分).
在图②中,将折线A1A2A3向右平移1个单位长度到折线B1B2B3的位置,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你画一条类似的有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出前三个图形中除去阴影部分后剩余部分的面积:S1,S2,S3;
(3)联想与探索:
如图④,在一块长方形草地上,草地的长和宽仍分别为a,b,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位长度),请你猜想空白部分表示的草地面积是多少,并说明你的猜想是正确的.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟免再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程),有下列说法:
①兔子和乌龟同时从起点出发;②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟; ④兔子比乌龟早10分钟到达终点.
其中正确的说法是_____(把你认为正确说法的序号都填上);
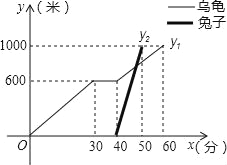
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com