
【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且交边CD于点E. 
(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2,若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.
【答案】
(1)证明:
如图1,过P作MN∥AD,交AB于M,交CD于N,
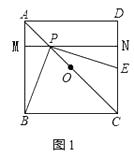
∵PB⊥PE,
∴∠BPE=90°,
∴∠MPB+∠EPN=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,
∵AD∥MN,
∴∠BMP=∠BAD=∠PNE=∠D=90°,
∴∠MPB+∠MBP=90°,
∴∠EPN=∠MBP,
Rt△PNC中,∠PCN=45°,
∴△PNC是等腰直角三角形,
∴PN=CN,
∵∠BMP=∠PNC=∠ABC=90°,
∴四边形MBCN是矩形,
∴BM=CN,
∴BM=PN,
∴△BMP≌△PNE(ASA),
∴PB=PE;
(2)解:在P点运动的过程中,PF的长度不发生变化,理由是:
如图2,连接OB,
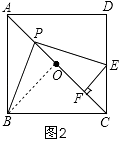
∵点O是正方形ABCD对角线AC的中点,
∴OB⊥AC,
∴∠AOB=90°,
∴∠AOB=∠EFP=90°,
∴∠OBP+∠BPO=90°,
∵∠BPE=90°,
∴∠BPO+∠OPE=90°,
∴∠OBP=∠OPE,
由(1)得:PB=PE,
∴△OBP≌△FPE,
∴PF=OB,
∵AB=2,△ABO是等腰直角三角形,
∴OB= ![]() =
= ![]() ,
,
∴PF为定值是 ![]() .
.
【解析】(1)作辅助线,构建全等三角形,根据ASA证明△BMP≌△PNE可得结论;(2)如图2,连接OB,通过证明△OBP≌△FPE,得PF=OB,则PF为定值是 ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,一次函数y=﹣x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.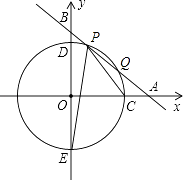
(1)若直线AB交劣弧 ![]() 于P、Q两点(异于C、D)
于P、Q两点(异于C、D)
①当P点坐标为(3,4)时,求b值;
②求∠CPE的度数,并用含b的代数式表示弦PQ的长(写出b的取值范围);
(2)当b=6时,线段AB上存在几个点F,使∠CFE=45°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜和甜瓜是新疆特色水果,小明的妈妈先购买了2千克西瓜和3千克甜瓜,共花费9元;后又购买了1千克西瓜和2千克甜瓜,共花费5.5元.(每次两种水果的售价都不变)
(1)求两种水果的售价分别是每千克多少元?
(2)如果还需购买两种水果共12千克,要求甜瓜的数量不少于西瓜数量的两倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2 ![]() )米.
)米. 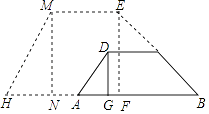
(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察等式:① ![]() =1﹣
=1﹣ ![]() ;②
;② ![]() =
= ![]() ﹣
﹣ ![]() ;③
;③ ![]() =
= ![]() ﹣
﹣ ![]() ;④
;④ ![]() =
= ![]() ﹣
﹣ ![]() ,…
,…
(1)试用字母n的等式表示出你发现的规律,并证明该等式成立;
(2)![]()
+ ![]() +
+ ![]() +…+
+…+ ![]() = . (直接写出结果)
= . (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因式分解是初中数学中一种重要的恒等变形,它具有广泛的应用,是解决许多数学问题的有力工具,例如,一个基本事实:“若ab=0,则a=0或b=0”,那么一元二次方程x2﹣x﹣2=0就可以通过因式分解转化为(x﹣2)(x+1)=0的形式,再由基本事实可得:x﹣2=0或x+1=0,所以方程有两个解为x=2,x=﹣1.
(1)试利用上述基本事实,解方程2x2﹣x=0;
(2)若(x2+y2)(x2+y2﹣1)﹣2=0,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() (a>0,a为常数)和y=
(a>0,a为常数)和y= ![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y= ![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y= ![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y= ![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y= ![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 .
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 . 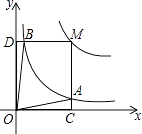
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“书香包河”读书活动中,学校准备购买一批课外读物,为使课外读物满足学生们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了______________名同学;
(2)条形统计图中,m=_________,n=__________;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com