
【题目】如图,平面直角坐标系xOy中,一次函数y=﹣x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.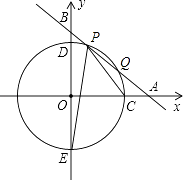
(1)若直线AB交劣弧 ![]() 于P、Q两点(异于C、D)
于P、Q两点(异于C、D)
①当P点坐标为(3,4)时,求b值;
②求∠CPE的度数,并用含b的代数式表示弦PQ的长(写出b的取值范围);
(2)当b=6时,线段AB上存在几个点F,使∠CFE=45°?请说明理由.
【答案】
(1)
解:①∵点P(3,4)在直线AB上,
∴﹣3+b=4,
∴b=7,②∵∠COE=90°,
∴∠CPE= ![]() ∠COE=45°,
∠COE=45°,
如图1,过点O作OM⊥AB于M,连接OP,

∵直线AB的解析式为y=﹣x+b①,
∴直线OM的解析式为y=x②,
联立①②解得点M( ![]() b,
b, ![]() b),
b),
∴OM2= ![]() b2,
b2,
在Rt△POM中,OP=5,根据勾股定理得,PM= ![]() =
= ![]() ,
,
∴PQ=2PM= ![]()
![]() ,
,
当点P和点D重合时,b=5
当OM=5时,b=﹣5 ![]() (舍)或b=5
(舍)或b=5 ![]() ,
,
∴5≤b<5 ![]() ,
,
即:PQ= ![]()
![]() (5≤b<5
(5≤b<5 ![]() )
)
(2)
解:当b=6时,线段AB上存在2个点F,使∠CFE=45°,
理由:由(1)②知,点F在劣弧 ![]() 上时,∠CFE=45°,
上时,∠CFE=45°,
由(1)②知,OM=5时,即:b=5 ![]() 时,直线AB与⊙O相切,
时,直线AB与⊙O相切,
当点B与点D重合时,b=5,
∴当b=6时,在5到5 ![]() 之间,
之间,
∴线段AB与⊙Q有两个交点,
即:当b=6时,线段AB上存在2个点F,使∠CFE=45°.
【解析】(1)①直接将点P的坐标代入直线y=﹣x+b中,即可求出b的值,②先求出直线OM的解析式,即可得出点M的坐标,进而得出OM,再用勾股定理即可得出PM,即可得出PQ;(2)先判断出点F是劣弧 ![]() 上时,∠CFE=45°,进而判断b=6是线段AB与⊙O的交点的个数即可得出结论.
上时,∠CFE=45°,进而判断b=6是线段AB与⊙O的交点的个数即可得出结论.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: ①所调查的七年级50名学生在这个月内做好事次数的平均数是 , 众数是 , 极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
【答案】解:①平均数;(2×5+3×6+4×13+5×16+6×10)÷50=4.4;
众数:5次;
极差:6﹣2=4;
②做好事不少于4次的人数:800× ![]() =624;
=624;
(1)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球. ①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?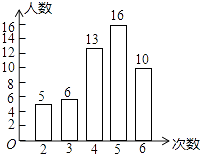
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
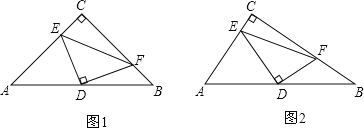
【题目】已知:如图1,Rt△ABC中,∠ACB=90°,D为AB中点,DE、DF分别交AC于E,交BC于F,且DE⊥DF.
(1)如果CA=CB,求证:AE2+BF2=EF2;
(2)如图2,如果CA<CB,(1)中结论还能成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为真命题的是
A.有两边及一角对应相等的两个三角形全等
B.方程x2+2x+3=0有两个不相等的实数根
C.面积之比为1∶2的两个相似三角形的周长之比是1∶4
D.顺次连接任意四边形各边中点得到的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且交边CD于点E. 
(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2,若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com