
分析 (1)首先将常数项移到等号的右侧,把二次项系数化为1,再将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.
(2)找出二次项系数,一次项系数及常数项,计算出根的判别式,发现其结果大于0,故利用求根公式可得出方程的两个解.
(3)此题可采用提公因式法,可得方程因式分解的形式,即可求解.
(4)原方程整理得x2+9x+20=0,然后分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)原方程变形为x2-$\frac{3}{2}$x=$\frac{3}{4}$
∴x2-$\frac{3}{2}$x+$\frac{9}{16}$=$\frac{3}{4}$+$\frac{9}{16}$
∴(x-$\frac{3}{4}$)=$\frac{21}{16}$
∴x-$\frac{3}{4}$=±$\frac{\sqrt{21}}{4}$.
∴x1=$\frac{3+\sqrt{21}}{4}$,x2=$\frac{3-\sqrt{21}}{4}$.
(2)2x2+5x-1=0,
∵a=2,b=5,c=-1,
∴b2-4ac=25+8=33>0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-5±\sqrt{33}}{2×2}$,
∴x1=$\frac{-5+\sqrt{33}}{4}$,x2=$\frac{-5-\sqrt{33}}{4}$.
(3)3x(x-1)=2-2x,
3x(x+1)+2(x-1)=0.
(x-1)(3x+2)=0.
∴x-1=0,3x+2=0,
解得 x1=1,x2=-$\frac{2}{3}$.
(4)(x+8)(x+1)=-12,
x2+9x+20=0,
(x+5)(x+4)=0,
∴x+5=0,x+4=0,
∴x1=-5,x2=-4.
点评 本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
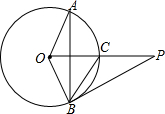 如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.
如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com