
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.
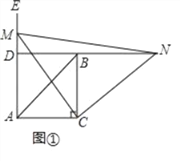

(1)问题发现:直接写出∠NDE= 度;
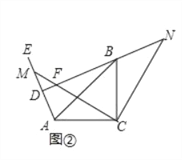
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.
(3)如图③,若∠EAC=15°,BD=![]() ,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
【答案】(1)90°;
(2)证明见解析;
(3)AC=2.
【解析】分析:(1)根据题意证明△MAC≌△NBC即可;(2)∠NDE的大小不变,证明△MAC≌△NBC,得到∠N=∠AMC,又∠MFD=∠NFC,所以∠MDF=∠FCN=90°,即∠NDE=90°.(3)先证明△MAC≌△NBC,所以∠NBC=∠MAC=15°,再证明∠BDH=∠ACH=90°,∠ABD=60°,求出AB=2![]() ,根据AC=ABcos45°,即可解答.
,根据AC=ABcos45°,即可解答.
本题解析:
(1)∵∠ACB=90°,∠MCN=90°,∴∠ACM=∠BCN,
在△MAC和△NBC中,
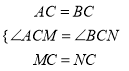 ,∴△MAC≌△NBC,∴∠NBC=∠MAC=90°,
,∴△MAC≌△NBC,∴∠NBC=∠MAC=90°,
又∵∠ACB=90°,∠EAC=90°,∴∠NDE=90°.
故答案为:90°.
(2)∠NDE的大小不变,
在△MAC和△NBC中,
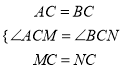 ,∴△MAC≌△NBC,∴∠N=∠AMC,
,∴△MAC≌△NBC,∴∠N=∠AMC,
又∵∠MFD=∠NFC,∴∠MDF=∠FCN=90°,即∠NDE=90°.
(3)AC=2,
在△MAC和△NBC中,
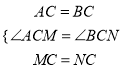 ,
,
∴△MAC≌△NBC,∴∠NBC=∠MAC=15°,
如图③,设BC与AD交于点H,
又∵∠AHC=∠BHD,∴∠BDH=∠ACH=90°,
∴在Rt△ABD中,∠ABD=∠ABC+∠NBC=45°+15°=60°
∵BD=![]() ,∴AB=2
,∴AB=2![]() ,
,
∴AC=ABcos45°=2.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
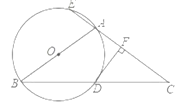
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示: 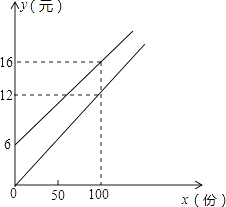
(1)填空:甲种收费的函数关系式是 . 乙种收费的函数关系式是 .
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com