
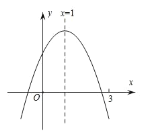
【题目】二次函数yax2bxca0图象如图所示,下列结论:①abc0;②2ab0;③当m1时,abam2bm;④abc0;⑤若![]()
![]() ,且
,且![]() ,则
,则![]() ,其中正确的有( )
,其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据抛物线开口方向得a<0,由抛物线对称轴为直线![]() ,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-1,0)的右侧,则当x=-1时,y<0,所以a-b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1-x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即
,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-1,0)的右侧,则当x=-1时,y<0,所以a-b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1-x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即![]() ,然后把b=-2a代入计算得到x1+x2=2.
,然后把b=-2a代入计算得到x1+x2=2.
解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线![]() ,
,
∴b=-2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③正确;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(-1,0)的右侧
∴当x=-1时,y<0,
∴a-b+c<0,所以④错误;
∵ax12+bx1=ax22+bx2,
∴ax12+bx1-ax22-bx2=0,
∴a(x1+x2)(x1-x2)+b(x1-x2)=0,
∴(x1-x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即![]()
∵b=-2a,
∴x1+x2=2,所以⑤正确.
综上所述,正确的有②③⑤.
故选:C.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作观察)任意一张三角形纸片有3个顶点。
第1次在它的内部增画1个点,此时三角形纸片内部共有1个点;
第2次在它的内部继续增画2个点,此时三角形纸片内部共有1+2=3个点;
第3次在它的内部继续增画3个点,此时三角形纸片内部共有1+2+3=6个点;
……
第![]() 次在它的内部继续增画
次在它的内部继续增画![]() 个点,此时三角形纸片内部共有
个点,此时三角形纸片内部共有![]() 个点。
个点。
(动手实践)
第![]() 次画点后,在三角形纸片内部共有
次画点后,在三角形纸片内部共有![]() 个点,以
个点,以![]() 个点为顶点,把三角形纸片剪成若干个小三角形纸片,设最多可以剪得
个点为顶点,把三角形纸片剪成若干个小三角形纸片,设最多可以剪得![]() 个这样的小三角形。
个这样的小三角形。
(思考解答)
(1)第![]() 次画点后,
次画点后,![]() __________________;(用含有
__________________;(用含有![]() 的代数式表示);
的代数式表示);
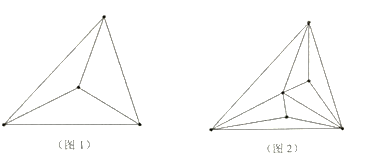
(2)第1次画点后,如图1,以4个点为顶点,将原三角形纸片剪成若干个小三角形,最多可以剪得3个这样的小三角形,所以![]() ;第2次画点后,如图2,以6个点为顶点,最多可以剪得7个这样的小三角形,所以
;第2次画点后,如图2,以6个点为顶点,最多可以剪得7个这样的小三角形,所以![]() ;第3次画点后,以9个点为顶点,可得
;第3次画点后,以9个点为顶点,可得![]() ____________________;
____________________;
(3)第![]() 次画点后,可得
次画点后,可得![]() ______________;(用含有
______________;(用含有![]() 的代数式表示);
的代数式表示);
(4)第![]() 次画点后,可得
次画点后,可得![]() 个小三角形,第
个小三角形,第![]() 次画点后,可得
次画点后,可得![]() 个小三角形,则
个小三角形,则![]() ________________________。(用含有
________________________。(用含有![]() 的代数式表示)。
的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2019个格子中的数为_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
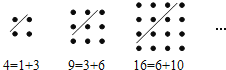
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A9m,0、Bm,0m0,以AB为直径的⊙M交y轴正半轴于点C,CD是⊙M的切线,交x轴正半轴于点D,过A作AECD于E,交⊙于F.
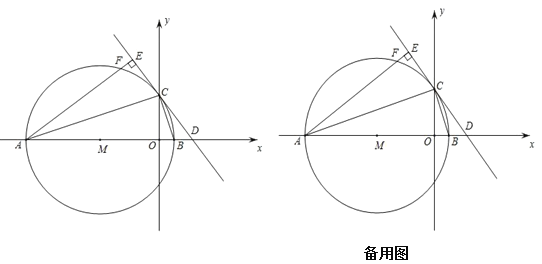
(1)求C的坐标;(用含m的式子表示)
(2)①请证明:EFOB;②用含m的式子表示AFC的周长;
(3)若![]() ,
,![]() ,
,![]() 分别表示
分别表示![]() 的面积,记
的面积,记![]() ,对于经过原点的二次函数
,对于经过原点的二次函数![]() ,当
,当![]() 时,函数y的最大值为a,求此二次函数的解析式.
时,函数y的最大值为a,求此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
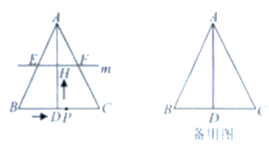
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 的速度向点
的速度向点![]() 匀速运动;与此同时,垂直于
匀速运动;与此同时,垂直于![]() 的直线
的直线![]() 从底边
从底边![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 方向匀速平移,分别交
方向匀速平移,分别交![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() ,当点
,当点![]() 到达点
到达点![]() 时,点
时,点![]() 与直线
与直线![]() 同时停止运动,设运动时间为
同时停止运动,设运动时间为![]() 秒(
秒(![]() ).
).
(1)当![]() 时,连接
时,连接![]() 、
、![]() ,求证:四边形
,求证:四边形![]() 为菱形;
为菱形;
(2)当![]() 时,求
时,求![]() 的面积;
的面积;
(3)是否存在某一时刻![]() ,使
,使![]() 为以点
为以点![]() 或
或![]() 为直角顶点的直角三角形?若存在,请求出此时刻
为直角顶点的直角三角形?若存在,请求出此时刻![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
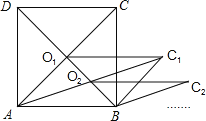
【题目】如图所示,矩形ABCD的面积为10cm2,它的两条对角线交于点O1,以AB、AO1为邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC5O5的面积为( )
A. 1cm2B. 2cm2C. ![]() cm2D.
cm2D. ![]() cm2
cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com