
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() .��
.��![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ����ÿ��
����ÿ��![]() ���ٶ����
���ٶ����![]() �����˶������ͬʱ����ֱ��
�����˶������ͬʱ����ֱ��![]() ��ֱ��
��ֱ��![]() �ӵױ�
�ӵױ�![]() ��������ÿ��
��������ÿ��![]() ���ٶ���
���ٶ���![]() ��������ƽ�ƣ��ֱ�
��������ƽ�ƣ��ֱ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() �����
�����![]() ʱ����
ʱ����![]() ��ֱ��
��ֱ��![]() ͬʱֹͣ�˶������˶�ʱ��Ϊ
ͬʱֹͣ�˶������˶�ʱ��Ϊ![]() �루
�루![]() ��.
��.
��1����![]() ʱ������
ʱ������![]() ��
��![]() ����֤���ı���
����֤���ı���![]() Ϊ���Σ�
����
��2����![]() ʱ����
ʱ����![]() �������
�������
��3���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() Ϊ�Ե�
Ϊ�Ե�![]() ��
��![]() Ϊֱ�Ƕ����ֱ�������Σ������ڣ��������ʱ��
Ϊֱ�Ƕ����ֱ�������Σ������ڣ��������ʱ��![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
���𰸡���1������������2��![]() ����3�������Ե�
����3�������Ե�![]() Ϊֱ�Ƕ����ֱ��������.��ʱ��
Ϊֱ�Ƕ����ֱ��������.��ʱ��![]() .
.
��������
��1���������ε��ж�����������⣻
��2���ɣ�1��֪![]() ����
����![]() ����
���� ![]() �������
�������![]() ��
��
![]() �� �ٸ��������ε������ʽ������⣻
�� �ٸ��������ε������ʽ������⣻
��3�����������������![]() Ϊֱ�Ƕ��㣬 ������
Ϊֱ�Ƕ��㣬 ������![]() Ϊֱ�Ƕ��㣬 �������������ε����ʼ������.
Ϊֱ�Ƕ��㣬 �������������ε����ʼ������.
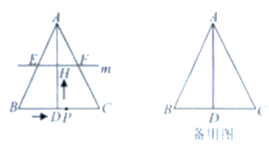
��1��֤������ͼ1����![]() ʱ��
ʱ��![]() ��
��
��![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ��
��
��![]() Ϊ
Ϊ![]() �Ĵ�ֱƽ���ߣ���
�Ĵ�ֱƽ���ߣ���![]() ��
��![]() .
.
��![]() ����
����![]() .
.
��![]() ����
����![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() �����ı���
�����ı���![]() Ϊ����.
����.
��2����ͼ2���ɣ�1��֪![]() ��
��
��![]() ��
��
��![]() ����
����![]() ����ã�
����ã�![]() ��
��
![]() ��
��
![]() ��
��
��3��������![]() Ϊֱ�Ƕ��㣬��ͼ3����
Ϊֱ�Ƕ��㣬��ͼ3����
��ʱ![]() ��
��![]() ��
��![]() .
.
��![]() ����
����![]() ��
��
����![]() ���˱���ʽ���������ʲ������Ե�
���˱���ʽ���������ʲ������Ե�![]() Ϊֱ�Ƕ����ֱ�������Σ�
Ϊֱ�Ƕ����ֱ�������Σ�
������![]() Ϊֱ�Ƕ��㣬��ͼ3����
Ϊֱ�Ƕ��㣬��ͼ3����
��ʱ![]() ��
��![]() ��
��![]() ��
��![]() .
.
��![]() ����
����![]() ������
������![]() ��
��
���![]() .�ʴ����Ե�
.�ʴ����Ե�![]() Ϊֱ�Ƕ����ֱ��������.��ʱ��
Ϊֱ�Ƕ����ֱ��������.��ʱ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
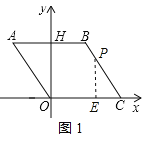
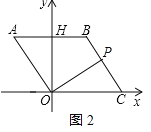
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬�ı���ABCO�����Σ���C��x����������ϣ�AB�߽�y���ڵ�H��OC��4����BCO��60����
��1�����A������
��2������P�ӵ�A������������A��BһC�ķ�����2����λ��������ٶ����յ�C�����˶������POC�����ΪS����P���˶�ʱ��Ϊt�룬��S��t֮��ĺ�����ϵʽ��Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�ֱ��д����tΪ��ֵʱ��POCΪֱ�������Σ�
 ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���yax2bxca0ͼ����ͼ��ʾ�����н��ۣ���abc0����2ab0���۵�m1ʱ��abam2bm����abc0������![]()
![]() ����
����![]() ����
����![]() ��������ȷ���У� ��
��������ȷ���У� ��
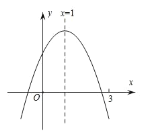
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1��12��(��16)+(��4)��5
��2��![]()
��3��![]()
��4��(8a-7b)-(4a-5b)
��5��![]()
��6���Ȼ�������ֵ��![]() �� ����
�� ����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������A ����������ӻ��ְ����£�
���� | �������� | ʤ�� | ���� | ���� |
��һ˫¹ | 20 | 18 | 2 | 38 |
������ | 20 | 14 | 6 | 34 |
�㽭���� | 20 | 7 | 13 | 27 |
����ʨ | 20 | 0 | 20 | 20 |
��1���ñ���ʤ1���Ļ���Ϊ �֣���1���Ļ���Ϊ �֣� ��ʽ��ʾ������ʤ��������֮���������ϵ������ʤ����Ϊm��������α����Ļ����� ��ֱ��д�������
��2��ij�ӵ�ʤ���ܻ����ܵ������ĸ����ܻ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���ax2+bx+c=0��a��0���У�����˵����
����a+b+c=0����b2��4ac��0��
��������������1��2����2a+c=0��
��������ax2+c=0����������ȵ�ʵ������ax2+bx+c=0������������ȵ�ʵ����
����b=2a+c��������������ȵ�ʵ����������ȷ���У�������
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����̨��һ�������Խ�Ŀ�У�����ϷPK���ڣ�Ϊ�������ѡ��Ϸ˫������Ա�������������������Ϸ���ò����İײ���ס������ɫ������ͬ��ϸ��AA1��BB1��CC1��ֻ¶�����ǵ�ͷ��β����ͼ��ʾ�����ɼס�����λ�α��ֱ�Ӱײ����˸�ѡһ��ϸ������������������ѡ��ͬһ��ϸ����������ͬ�ӣ�����Ϊ������Ա��
��1�����α���������ѡ��һ��ϸ������������ǡ�ó��ϸ��AA1�ĸ��ʣ�
��2�����û���״ͼ�����б�������ס�����λ�α��ܷ�Ϊͬ�ӵĸ��ʣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��![]() ��
��![]() ����ͬʱ������������ʻ����֪�׳����ٶȴ����ҳ����ٶȣ��׳�����
����ͬʱ������������ʻ����֪�׳����ٶȴ����ҳ����ٶȣ��׳�����![]() �غ���������һ�ٶ�ԭ·����
�غ���������һ�ٶ�ԭ·����![]() ��(��ͷ��ʱ����Բ���)���ҳ�����
��(��ͷ��ʱ����Բ���)���ҳ�����![]() ���Ժ�ͣ��
���Ժ�ͣ��![]() �صȴ��׳�����ͼ��ʾΪ����������ľ���
�صȴ��׳�����ͼ��ʾΪ����������ľ���![]() (ǧ��)��׳�����ʻʱ��
(ǧ��)��׳�����ʻʱ��![]() (Сʱ)֮��ĺ���ͼ�����ҳ�����
(Сʱ)֮��ĺ���ͼ�����ҳ�����![]() �ص�ʱ�׳���
�ص�ʱ�׳���![]() �صľ���Ϊ__________ǧ�ף�
�صľ���Ϊ__________ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
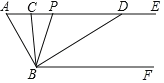
����Ŀ����ͼ����֪AE��BF����A=60�㣬��PΪ����AE������һ�㣨�����A�غϣ���BC��BD�ֱ�ƽ�֡�ABP�͡�PBF��������AE�ڵ�C����D��
��1��ͼ�С�CBD= �㣻
��2������ACB=��ABDʱ����ABC= �㣻
��3�����Pλ�õı仯��ͼ�С�APB���ADB֮���������ϵʼ��Ϊ ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com