
����Ŀ��ij���������A ����������ӻ��ְ����£�
���� | �������� | ʤ�� | ���� | ���� |
��һ˫¹ | 20 | 18 | 2 | 38 |
������ | 20 | 14 | 6 | 34 |
�㽭���� | 20 | 7 | 13 | 27 |
����ʨ | 20 | 0 | 20 | 20 |
��1���ñ���ʤ1���Ļ���Ϊ �֣���1���Ļ���Ϊ �֣� ��ʽ��ʾ������ʤ��������֮���������ϵ������ʤ����Ϊm��������α����Ļ����� ��ֱ��д�������
��2��ij�ӵ�ʤ���ܻ����ܵ������ĸ����ܻ�����
���𰸡���1�� 2 1 ��m+20���֣�2��m=![]() ����
����
��������
��1����ʤһ����x�֣���һ����y�֣��г���Ԫһ�η����飬���ɵõ��𰸣���ʤ��Ϊmʱ����ʽ���㣬���ɵõ�����ʽ��
��2�������ܻ��ֵĹ�ϵ���г����̣����m��ʵ��������з�������.
�⣺��1����ʤһ����x�֣���һ����y�֣��������⣬�ã�
![]() ����ã�
����ã�![]() ��
��
��ñ���ʤ1���Ļ���Ϊ2�֣���1���Ļ���Ϊ1�֣�
������ʤ����Ϊm��ʱ�����ܻ���Ϊ��
![]() ��
��
�ʴ�Ϊ��2��1����![]() ����.
����.
��2����ij�ӵ�ʤ���ܻ��ֵ������ĸ����ܻ��֣���
![]() ��
��
��ã�![]() ��
��
��m�������������������⣮
��ij�ӵ�ʤ���ܻ��ֲ��ܵ������ĸ����ܻ���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[x]��ʾ������x������������磬[��]=3��[2]=2��[��2.1]=��3�������н��ۣ�
��[��x]=��[x]��
����[x]=n����x��ȡֵ��Χ��n��x��n+1��
�۵���1��x��1ʱ��[1+x]+[1��x]��ֵΪ1��2��
��x=��2.75�Ƿ���4x��2[x]+5=0��Ψһһ���⣮
������ȷ�Ľ�����_____��д��������ȷ���۵���ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����±�����������ÿ��С�����ж�����һ��������ʹ�����������������ڸ�������������֮�Ͷ���ȣ����2019�������е���Ϊ_________________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A9m,0��Bm,0m0����ABΪֱ���ġ�M��y���������ڵ�C��CD�ǡ�M�����ߣ���x���������ڵ�D����A��AECD��E��������F.
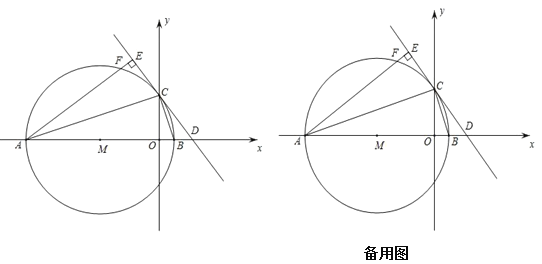
��1����C�����ꣻ���ú�m��ʽ�ӱ�ʾ��
��2������֤����EFOB�����ú�m��ʽ�ӱ�ʾAFC���ܳ���
��3����![]() ��
��![]() ��
��![]() �ֱ��ʾ
�ֱ��ʾ![]() ���������
���������![]() �����ھ���ԭ��Ķ��κ���
�����ھ���ԭ��Ķ��κ���![]() ����
����![]() ʱ������y�����ֵΪa����˶��κ����Ľ���ʽ.
ʱ������y�����ֵΪa����˶��κ����Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ����ͬѧ�ǿ���������Ҫ��������������ɸ�����֪����ĵ��۱�����ĵ��۶�30Ԫ����500Ԫ���õ�������������800Ԫ���õ�����������ȣ�
��1�����������ĵ��۸��Ƕ���Ԫ��
��2����ǡ����ȥ1200Ԫ�����ļ��ֹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() .��
.��![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ����ÿ��
����ÿ��![]() ���ٶ����
���ٶ����![]() �����˶������ͬʱ����ֱ��
�����˶������ͬʱ����ֱ��![]() ��ֱ��
��ֱ��![]() �ӵױ�
�ӵױ�![]() ��������ÿ��
��������ÿ��![]() ���ٶ���
���ٶ���![]() ��������ƽ�ƣ��ֱ�
��������ƽ�ƣ��ֱ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() �����
�����![]() ʱ����
ʱ����![]() ��ֱ��
��ֱ��![]() ͬʱֹͣ�˶������˶�ʱ��Ϊ
ͬʱֹͣ�˶������˶�ʱ��Ϊ![]() �루
�루![]() ��.
��.
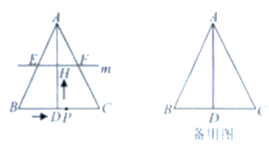
��1����![]() ʱ������
ʱ������![]() ��
��![]() ����֤���ı���
����֤���ı���![]() Ϊ���Σ�
����
��2����![]() ʱ����
ʱ����![]() �������
�������
��3���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() Ϊ�Ե�
Ϊ�Ե�![]() ��
��![]() Ϊֱ�Ƕ����ֱ�������Σ������ڣ��������ʱ��
Ϊֱ�Ƕ����ֱ�������Σ������ڣ��������ʱ��![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4��BC=2��OΪ�Խ���AC���е㣬��P��Q�ֱ��A��B����ͬʱ�������ڱ�AB��BC�������˶�������ͬʱ�����յ�B��C������PO��QO���ӳ��ֱ���CD��DA���ڵ�M��N���������˶������У�ͼ����Ӱ��������Ĵ�С�仯������� ��
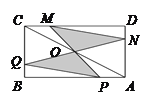
A. һֱ���� B. һֱ��С C. �ȼ�С������ D. ��������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
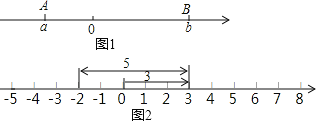
����Ŀ���Ķ����ϣ���ͼ1��ʾ����A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB=|a��b|�����磺|5������2��|��ʾ5�멁2֮��ľ���ֵ��ʵ����Ҳ������Ϊ5�멁2����������������Ӧ������֮��ľ��룮
��1����ͼ2��ʾ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�3����λ���ȣ��������ƶ�5����λ���ȣ����Կ����յ��ʾ�����ǩ�2���������ν��˼�룬�������ͼ��˼����������и��⣺
�������ϱ�ʾ2�멁5������֮��ľ������� ������λ���ȣ�
���������ϵĵ�A��ʾ����Ϊx����B��ʾ����Ϊ��1����A��B����ľ�����Ա�ʾΪ�� ������|x+1|=3����xΪ�� ����
�������A��ʾ����1����A�������ƶ�18����λ���ȣ��������ƶ�13����λ�����յ�ΪB����ôA��B�����ľ������� ����
��2���������ϵĵ�A��ʾ����Ϊx��xΪ��������xΪ�� ��ʱ��|x+5|��|x��7|��ֵ��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݰ���˹̹������ۿ�֪���κ�������˶��ٶȲ��ܳ������٣�3��105km/s������Ϊһ������ﵽ������Ҫ����������������ʱ��ᵹ����������ʵ���Dz����ܵģ������ǿ���һ�������ﳬ�����˶������磺ֱ��l��m��ʾ����ľ���ཻ�ɵ���ǵĶ���Ϊ10�������Ƿֱ�����������ֱ�ķ���������ƽ��ʱ�����ǵĽ���AҲ�����ƶ�����ͼ��ͷ��ʾ�����������ֱ�ߵ��ƶ��ٶȶ��ǹ��ٵ�0.2������A���ƶ��ٶ��ǹ��ٵ�_____�������������������Ч���֣���
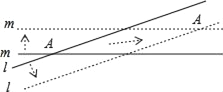
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com