
ЁОЬтФПЁПФГЩЬГЁЙКНјвЛХњ 30 ЭпЕФ LED ЕЦХнКЭЦеЭЈАзГуЕЦХнНјааЯњЪлЃЌЦфНјМлгыБъМлШчЯТБэЃК
LED ЕЦХн | ЦеЭЈАзГуЕЦХн | |
НјМлЃЈдЊЃЉ | 45 | 25 |
БъМлЃЈдЊЃЉ | 60 | 30 |

ЃЈ1ЃЉИУЩЬГЁЙКНјСЫ LED ЕЦХнгыЦеЭЈАзГуЕЦХнЙВ 300 ИіЃЌLED ЕЦХнАДБъМлНјааЯњЪлЃЌЖјЦеЭЈ АзГуЕЦХнДђОХелЯњЪлЃЌЕБЯњЪлЭъетХњЕЦХнКѓПЩЛёРћ 3 200 дЊЃЌЧѓИУЩЬГЁЙКНј LED ЕЦХнгы ЦеЭЈАзГуЕЦХнЕФЪ§СПЗжБ№ЮЊЖрЩйИіЃП
ЃЈ2ЃЉгЩгкДКНкЦкМфШШЯњЃЌКмПьНЋСНжжЕЦХнЯњЪлЭъЃЌШєИУЩЬГЁМЦЛЎдйДЮЙКНјетСНжжЕЦХн 120 ИіЃЌ дкВЛДђелЕФЧщПіЯТЃЌЧыЮЪШчКЮНјЛѕЃЌЯњЪлЭъетХњЕЦХнЪБЛёРћзюЖрЧвВЛГЌЙ§НјЛѕМлЕФ 30%ЃЌ ВЂЧѓГіДЫЪБетХњЕЦХнЕФзмРћШѓЮЊЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉLEDЕЦХнгыЦеЭЈАзГуЕЦХнЕФЪ§СПЗжБ№ЮЊ200ИіКЭ100ИіЃЛЃЈ2ЃЉ1 350дЊ.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшИУЩЬГЁЙКНјLEDЕЦХнxИіЃЌЦеЭЈАзГуЕЦХнЕФЪ§СПЮЊyИіЃЌРћгУИУЩЬГЁЙКНјСЫLEDЕЦХнгыЦеЭЈАзГуЕЦХнЙВ300ИіКЭЯњЪлЭъетХњЕЦХнКѓПЩвдЛёРћ3200дЊСаЗНГЬзщЃЌШЛКѓНтЗНГЬзщМДПЩЃЛ
ЃЈ2ЃЉЩшИУЩЬГЁЙКНјLEDЕЦХнaИіЃЌдђЙКНјЦеЭЈАзГуЕЦХнЃЈ120ЉaЃЉИіЃЌетХњЕЦХнЕФзмРћШѓЮЊWдЊЃЌРћгУРћШѓЕФвтвхЕУЕНW=ЃЈ60Љ45ЃЉa+ЃЈ30Љ25ЃЉЃЈ120ЉaЃЉ=10a+600ЃЌдйИљОнЯњЪлЭъетХњЕЦХнЪБЛёРћзюЖрЧвВЛГЌЙ§НјЛѕМлЕФ30%ПЩШЗЖЈaЕФЗЖЮЇЃЌШЛКѓИљОнвЛДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЩшИУЩЬГЁЙКНјLEDЕЦХнxИіЃЌЦеЭЈАзГуЕЦХнЕФЪ§СПЮЊyИіЃЌИљОнЬтвтЕУЃК
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
Д№ЃКИУЩЬГЁЙКНјLEDЕЦХнгыЦеЭЈАзГуЕЦХнЕФЪ§СПЗжБ№ЮЊ200ИіКЭ100ИіЃЛ
ЃЈ2ЃЉЩшИУЩЬГЁЙКНјLEDЕЦХнaИіЃЌдђЙКНјЦеЭЈАзГуЕЦХнЃЈ120ЉaЃЉИіЃЌетХњЕЦХнЕФзмРћШѓЮЊWдЊЃЌИљОнЬтвтЕУЃК
W=ЃЈ60Љ45ЃЉa+ЃЈ30Љ25ЃЉЃЈ120ЉaЃЉ=10a+600
Ёп10a+600Ём[45a+25ЃЈ120ЉaЃЉ]ЁС30%ЃЌНтЕУaЁм75ЃЎЁпk=10ЃО0ЃЌЁрWЫцaЕФдіДѓЖјдіДѓЃЌЁрa=75ЪБЃЌWзюДѓЃЌзюДѓжЕЮЊ1350ЃЌДЫЪБЙКНјЦеЭЈАзГуЕЦХнЃЈ120Љ75ЃЉ=45ИіЃЎ
Д№ЃКИУЩЬГЁЙКНјLEDЕЦХн75ИіЃЌдђЙКНјЦеЭЈАзГуЕЦХн45ИіЃЌетХњЕЦХнЕФзмРћШѓЮЊ1350дЊЃЎ


 ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ
ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ ШЋФмДГЙи100ЗжЯЕСаД№АИ
ШЋФмДГЙи100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыЭЌбЇУЧЭъГЩЯТСаМзЃЌввСНжжЩЬЦЗДгАќзАЕНЯњЪлЕФвЛЯЕСаЮЪЬтЃЛ
ЃЈ1ЃЉФГАќзАГЕМфга22УћЙЄШЫЃЌУПШЫУПаЁЪБПЩвдАќзА120ИіМзЩЬЦЗЛђеп200ИіввЩЬЦЗЃЌЧв1ИіМзЩЬЦЗашвЊДюХф2ИіввЩЬЦЗзАЯфЃЌЮЊЪЙУПЬьАќзАЕФМзЩЬЦЗКЭввЩЬЦЗИеКУХфжУЃЌгІАВХХАќзАМзЩЬЦЗКЭввЩЬЦЗЕФЙЄШЫИїЖрЩйУћЃП
ЃЈ2ЃЉФГЩчЧјГЌЪаЕквЛДЮгУ6000дЊЙКНјвЛХњМзЁЂввСНжжЩЬЦЗЃЌЦфжаМзЩЬЦЗЕФМўЪ§БШввЩЬЦЗМўЪ§ЕФ2БЖЩй30МўЃЌСНжжЩЬЦЗЕФНјМлКЭЪлМлШчЯТЭМЫљЪОЃК
Мз | вв | |
НјМлЃЈдЊ/МўЃЉ | 22 | 30 |
ЪлМлЃЈдЊ/МўЃЉ | 29 | 40 |
ЂйГЌЪаНЋетХњЛѕШЋВПЪлГівЛЙВПЩвдЛёРћЖрЩйдЊЃП
ЂкИУГЌЪаЕкЖўДЮЗжБ№вдЕквЛДЮЭЌбљЕФНјМлЙКНјЕкЖўХњМзЁЂввСНжжЩЬЦЗЃЌЦфжаввЩЬЦЗЕФМўЪ§ЪЧЕквЛХњввЩЬЦЗМўЪ§ЕФ3БЖЃЌМзЩЬЦЗЕФМўЪ§ВЛБфЃЌМзЩЬЦЗАДеедЪлМлЯњЪлЃЌввЩЬЦЗдкдМлЕФЛљДЁЩЯДђелЯњЪлЃЌЕкЖўХњЩЬЦЗШЋВПЪлГіКѓЛёЕУЕФзмРћШѓБШЕквЛХњЛёЕУЕФзмРћШѓЖр720дЊЃЌЧѓЕкЖўХњввЩЬЦЗдкдМлЛљДЁЩЯДђМИелЯњЪлЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊBDЪЧABCDЖдНЧЯпЃЌAEЁЭBDгкЕуEЃЌCFЁЭBDгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁеЁїCBFЃЛ
ЃЈ2ЃЉСЌНсCEЃЌAFЃЌЧѓжЄЃКЫФБпаЮAFCEЮЊЦНааЫФБпаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌМКжЊЯпЖЮAB=20cmЃЌCD=2cmЃЌЯпЖЮ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЃЌ
ЩЯдЫЖЏЃЌ![]() ЗжБ№ЪЧACЃЌBCЕФжаЕу.
ЗжБ№ЪЧACЃЌBCЕФжаЕу.
(1)Шє![]() =4cmЃЌдђ
=4cmЃЌдђ![]() =______cm.
=______cm.
(2)ЕБЯпЖЮ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЪБЃЌЪдХаЖЯ
ЩЯдЫЖЏЪБЃЌЪдХаЖЯ![]() ЕФГЄЖШЪЧЗёЗЂЩњБфЛЏ?ШчЙћВЛБфЧыЧѓГі
ЕФГЄЖШЪЧЗёЗЂЩњБфЛЏ?ШчЙћВЛБфЧыЧѓГі![]() ЕФГЄЖШЃЌШчЙћБфЛЏЃЌЧыЫЕУїРэгЩ.
ЕФГЄЖШЃЌШчЙћБфЛЏЃЌЧыЫЕУїРэгЩ.
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЧыдФЖСЯТСаВФСЯЃЌВЂНтД№ЯргІЕФЮЪЬтЃК
НЋШєИЩИіЪ§зщГЩвЛИіе§ЗНаЮЪ§еѓЃЌШєШЮвтвЛааЃЌвЛСаМАЖдНЧЯпЩЯЕФЪ§зжжЎКЭЖМЯрЕШЃЌдђГЦОпгаетжжаджЪЕФЪ§зжЗНеѓЮЊЁАЛУЗНЁБжаЙњЙХДњГЦЁАЛУЗНЁБЮЊЁАКгЭМЁАЁЂЁАТхЪщЁАЕШЃЌР§ШчЃЌЯТУцЪЧШ§ИіШ§НзЛУЗНЃЌЪЧНЋЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6ЃЌ7ЃЌ8ЃЌ9ЬюШыЕН3ЁС3ЕФЗНИёжаЕУЕНЕФЃЌЦфУПааЁЂУПСаЁЂУПЬѕЖдНЧЯпЩЯЕФШ§ИіЪ§жЎКЭЯрЕШЃЎ
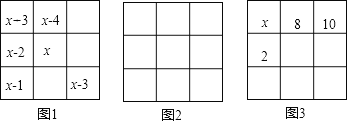
ЃЈ1ЃЉЩшЭМ1ЕФШ§НзЛУЗНжаМфЕФЪ§зжЪЧxЃЌгУxЕФДњЪ§ЪНБэЪОЛУЗНжа9ИіЪ§ЕФКЭЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧыФуНЋЯТСаОХИіЪ§ЃКЉ10ЁЂЉ8ЁЂЉ6ЁЂЉ4ЁЂЉ2ЁЂ0ЁЂ2ЁЂ4ЁЂ6ЗжБ№ЬюШыЭМ2ЗНИёжаЃЌЪЙЕУУПааЁЂУПСаЁЂУПЬѕЖдНЧЯпЩЯЕФШ§ИіЪ§жЎКЭЖМЯрЕШЃЛ
ЃЈ3ЃЉЭМ3ЪЧвЛИіШ§НзЛУЗНЃЌФЧУДБъгаxЕФЗНИёжаЫљЬюЕФЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ4ЃЉШчЭМ4ЫљЪОЕФУПвЛИідВжаЗжБ№ЬюаДСЫ1ЁЂ2ЁЂ3Ё19жаЕФвЛИіЪ§зжЃЈВЛЭЌЕФдВжаЬюаДЕФЪ§зжИїВЛЯрЭЌЃЉЃЌЪЙЕУЭМжаУПвЛИіКсЛђаБЗНЯђЕФЯпЖЮЩЯМИИідВФкЕФЪ§жЎКЭЖМЯрЕШЃЌЯждквбжЊИУЭМжаЦпИідВФкЕФЪ§зжЃЌдђЭМжаЕФxЃНЁЁ ЁЁЃЌyЃНЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛБпЪЧСэвЛБпЕФ![]() БЖЕФШ§НЧаЮНазіжЧЛлШ§НЧаЮЃЌетСНБпжаНЯГЄБпГЦЮЊжЧЛлБпЃЌетСНБпЕФ МаНЧНазіжЧЛлНЧЃЎ
БЖЕФШ§НЧаЮНазіжЧЛлШ§НЧаЮЃЌетСНБпжаНЯГЄБпГЦЮЊжЧЛлБпЃЌетСНБпЕФ МаНЧНазіжЧЛлНЧЃЎ
ЃЈ1ЃЉдк RtЁїABC жаЃЌЁЯACBЃН90ЁуЃЌШєЁЯA ЮЊжЧЛлНЧЃЌдђЁЯB ЕФЖШЪ§ЮЊ ЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌдкЁїABC жаЃЌЁЯAЃН45ЁуЃЌЁЯBЃН30ЁуЃЌЧѓжЄЃКЁїABC ЪЧжЧЛлШ§НЧаЮЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌЁїABC ЪЧжЧЛлШ§НЧаЮЃЌBC ЮЊжЧЛлБпЃЌЁЯB ЮЊжЧЛлНЧЃЌAЃЈ3ЃЌ0ЃЉЃЌЕу BЃЌC дкКЏЪ§ yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯёЩЯЃЌЕу C дкЕу B ЕФЩЯЗНЃЌЧвЕу B ЕФзнзјБъЮЊ
ЃЈxЃО0ЃЉЕФЭМЯёЩЯЃЌЕу C дкЕу B ЕФЩЯЗНЃЌЧвЕу B ЕФзнзјБъЮЊ![]() ЃЎЕБЁїABCЪЧжБНЧШ§НЧаЮЪБЃЌЧѓ k ЕФжЕЃЎ
ЃЎЕБЁїABCЪЧжБНЧШ§НЧаЮЪБЃЌЧѓ k ЕФжЕЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃЌЛиД№ЯТСаЮЪЬтЃК
Ъ§жсЪЧбЇЯАгаРэЪ§ЕФвЛжжживЊЙЄОпЃЌШЮКЮгаРэЪ§ЖМПЩвдгУЪ§жсЩЯЕФЕуБэЪОЃЌетбљФмЙЛдЫгУЪ§аЮНсКЯЕФЗНЗЈНтОівЛаЉЮЪЬтЁЃР§ШчЃЌСНИігаРэЪ§дкЪ§жсЩЯЖдгІЕФЕужЎМфЕФОрРыПЩвдгУетСНИіЪ§ЕФВюЕФОјЖджЕБэЪОЃЛ
дкЪ§жсЩЯЃЌгаРэЪ§3гы1ЖдгІЕФСНЕужЎМфЕФОрРыЮЊ|31|=2ЃЛ
дкЪ§жсЩЯ,гаРэЪ§5гы2ЖдгІЕФСНЕужЎМфЕФОрРыЮЊ|5(2)|=7ЃЛ
дкЪ§жсЩЯЃЌгаРэЪ§2гы3ЖдгІЕФСНЕужЎМфЕФОрРыЮЊ|23|=5ЃЛ
дкЪ§жсЩЯ,гаРэЪ§8гы5ЖдгІЕФСНЕужЎМфЕФОрРыЮЊ|8(5)|=3ЃЛЁЁ
ШчЭМ1ЃЌдкЪ§жсЩЯгаРэЪ§aЖдгІЕФЕуЮЊЕуAЃЌгаРэЪ§bЖдгІЕФЕуЮЊЕуBЃЌAЃЌBСНЕужЎМфЕФОрРыБэЪОЮЊ|ab|Лђ|ba|ЃЌМЧЮЊ|AB|=|ab|=|ba|.

(1)Ъ§жсЩЯгаРэЪ§10гы5ЖдгІЕФСНЕужЎМфЕФОрРыЕШгк___ЃЛЪ§жсЩЯгаРэЪ§xгы5ЖдгІЕФСНЕужЎМфЕФОрРыгУКЌxЕФЪНзгБэЪОЮЊ___ЃЛШєЪ§жсЩЯгаРэЪ§xгы1ЖдгІЕФСНЕуAЃЌBжЎМфЕФОрРы|AB|=2ЃЌдђxЕШгк___ЃЛ
(2)ШчЭМ2ЃЌЕуMЃЌNЃЌPЪЧЪ§жсЩЯЕФШ§ЕуЃЌЕуMБэЪОЕФЪ§ЮЊ4ЃЌЕуNБэЪОЕФЪ§ЮЊ2ЃЌЖЏЕуPБэЪОЕФЪ§ЮЊx.
ЂйШєЕуPдкЕуMЃЌNжЎМфЃЌдђ|x+2|+|x4|=___ЃЛШє|x+2|+|x4|ЈT10ЃЌдђx=___ЃЛ
ЂкИљОндФЖСВФСЯМАЩЯЪіИїЬтЕФНтД№ЗНЗЈЃЌ|x+2|+|x|+|x2|+|x4|ЕФзюаЁжЕЕШгк___.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЕиЕФКЃАЮИпЖШЪЧ![]() УзЃЌввЕиЕФКЃАЮИпЖШБШМзЕиКЃАЮИпЖШЕФ
УзЃЌввЕиЕФКЃАЮИпЖШБШМзЕиКЃАЮИпЖШЕФ![]() БЖЖр
БЖЖр![]() УзЃЌБћЕиЕФКЃАЮИпЖШБШМзЕиКЃАЮИпЖШЕФ
УзЃЌБћЕиЕФКЃАЮИпЖШБШМзЕиКЃАЮИпЖШЕФ![]() БЖЩй
БЖЩй![]() УзЃЎ
УзЃЎ
(1) Ш§ЕиЕФКЃАЮИпЖШКЭвЛЙВЪЧЖрЩйУзЃПЃЛ
(2) ввЕиЕФКЃАЮИпЖШБШБћЕиЕФКЃАЮИпЖШИпЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
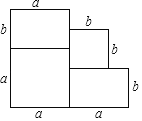
ЁОЬтФПЁПШчЭМЪЧвЛЫљзЁеЌЕФНЈжўЦНУцЭМЃЎ
ЃЈ1ЃЉгУКЌгаaЁЂbЕФЪНзгБэЪОетЫљзЁеЌЕФНЈжўУцЛ§ЃЎ
ЃЈ2ЃЉЕБaЃН5УзЃЌbЃН4УзЪБЃЌзЁеЌЕФНЈжўУцЛ§гаЖрДѓЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєДЫзЁеЌЕФЯњЪлЕЅМлЮЊУПЦНЗНУз5000дЊЃЌЧѓДЫзЁеЌЕФЯњЪлМлЪЧЖрЩйдЊЃПЃЈНсЙћгУПЦбЇМЧЪ§ЗЈБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com