
【题目】请同学们完成下列甲,乙两种商品从包装到销售的一系列问题;
(1)某包装车间有22名工人,每人每小时可以包装120个甲商品或者200个乙商品,且1个甲商品需要搭配2个乙商品装箱,为使每天包装的甲商品和乙商品刚好配置,应安排包装甲商品和乙商品的工人各多少名?
(2)某社区超市第一次用6000元购进一批甲、乙两种商品,其中甲商品的件数比乙商品件数的2倍少30件,两种商品的进价和售价如下图所示:
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
①超市将这批货全部售出一共可以获利多少元?
②该超市第二次分别以第一次同样的进价购进第二批甲、乙两种商品,其中乙商品的件数是第一批乙商品件数的3倍,甲商品的件数不变,甲商品按照原售价销售,乙商品在原价的基础上打折销售,第二批商品全部售出后获得的总利润比第一批获得的总利润多720元,求第二批乙商品在原价基础上打几折销售?
【答案】(1)应安排10名工人包装甲商品,12名工人包装乙商品;(2)①两种商品全部卖完可获得1950元利润;②第二次乙种商品是按原价打9折销售.
【解析】
(1)设应安排x名工人包装甲商品,则安排(22﹣x)人生产乙商品,根据生产的乙商品的数量是甲商品的2倍,即可得出关于x的一元一次方程,解之即可得出结论;
(2)①设第一次购进乙种商品m件,则购进甲种商品(2m﹣30)件,根据总价=单价×数量,即可得出关于m的一元一次方程,再利用总利润=每件的利润×销售数量即可求出销售总利润;
②设第二次乙种商品是按原价打y折销售,根据总利润=每件的利润×销售数量,即可得出关于y的一元一次方程,解之即可得出结论.
解:(1)设应安排x名工人包装甲商品,则安排(22﹣x)人生产乙商品,
依题意,得:200(22﹣x)=2×120x,
解得:x=10,
∴22﹣x=12.
答:应安排10名工人包装甲商品,12名工人包装乙商品.
(2)①设第一次购进乙种商品m件,则购进甲种商品(2m﹣30)件,
依题意,得:30m+22×(2m﹣30)=6000,
解得:m=90,
∴2m﹣30=150,
(29﹣22)×150+(40﹣30)×90=1950(元).
答:两种商品全部卖完可获得1950元利润.
②设第二次乙种商品是按原价打y折销售,
依题意,得:(29﹣22)×150+(40×![]() ﹣30)×90×3=1950+720,
﹣30)×90×3=1950+720,
解得:y=9.
答:第二次乙种商品是按原价打9折销售.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为(_______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏西15°的方向.
(1)∠AON= °;∠AOE= °;
(2)求∠WOB的补角及∠AOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
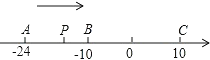
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA=________,PC=________;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,梯形ABCD中,AB∥CD,BC⊥AB,AB=AD,连接BD(如图a),点P沿梯形的边,从点A→B→C→D→A移动,设点P移动的距离为x,BP=y.
(1)求证:∠A=2∠CBD;
(2)当点P从点A移动到点C时,y与x的函数关系如图(b)中的折线MNQ所示,试求CD的长.
(3)在(2)的情况下,点P从A→B→C→D→A移动的过程中,△BDP是否可能为等腰三角形?若能,请求出所有能使△BDP为等腰三角形的x的取值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数a,B点表示数b,a、b满足|a+2|+|b﹣4|=0.
(1)点A表示的数为 ;点B表示的数为 ;
(2)一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离为 ;乙小球到原点的距离为 ;当t=3时,甲小球到原点的距离为 ;乙小球到原点的距离为 ;
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请求出甲,乙两小球到原点的距离相等时经历的时间.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED 灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了 LED 灯泡与普通白炽灯泡共 300 个,LED 灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利 3 200 元,求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120 个, 在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的 30%, 并求出此时这批灯泡的总利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com