
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为 ;
(2)如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;
(3)如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y=![]() (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为
(x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为![]() .当△ABC是直角三角形时,求 k 的值.
.当△ABC是直角三角形时,求 k 的值.


【答案】(1)45°.(2)见解析;(3)k=4![]() 或18+15
或18+15![]() .
.
【解析】试题分析:(1)由智慧角的定义得到AB=![]() AC,解直角三角形即可得到结论.
AC,解直角三角形即可得到结论.
(2)过点C作CD⊥AB于点D.在Rt△ACD中,由∠A=45°,得到AC=![]() DC.
DC.
在Rt△BCD中,由∠B=30°,得到BC=2DC,即可得到结论.
(3)分两种情况讨论:①∠ABC=90°;②∠BAC=90°.
试题解析:解:(1)∵∠ACB=90°,若∠A 为智慧角,∴AB=![]() AC,∴cosA=
AC,∴cosA=![]() ,∴∠A=45°,∴∠B=45°.
,∴∠A=45°,∴∠B=45°.
(2)如图1,过点C作CD⊥AB于点D.
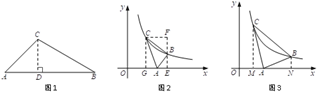
在Rt△ACD中,∠A=45°,∴AC=![]() DC.
DC.
在Rt△BCD中,∠B=30°,∴BC=2DC,∴![]() =
=![]() ,∴△ABC是智慧三角形.
,∴△ABC是智慧三角形.
(3)由题意可知:∠ABC=90°或∠BAC=90°.
①当∠ABC=90°时,如图2,过点B作BE⊥x轴于点E,过点C作CF⊥EB交EB延长线于点F,过点C作CG⊥x轴于点G,则∠AEB=∠F=∠ABC=90°,∴∠BCF+∠CBF=∠ABE+∠CBF=90°,∴∠BCF=∠ABE,∴△BCF∽△ABE,∴![]() =
=![]() =
=![]() =
=![]() .
.
设AE=a,则BF=![]() a.∵BE=
a.∵BE=![]() ,∴CF=2.
,∴CF=2.
∵OG=OA+AE-GE=3+a-2=1+a,CG=EF=![]() +
+![]() a,∴B(3+a,
a,∴B(3+a, ![]() ),C(1+a,
),C(1+a, ![]() +
+![]() a).∵点B,C在函数y=
a).∵点B,C在函数y=![]() (x>0)的图像上,∴
(x>0)的图像上,∴![]() (3+a)=(1+a)(
(3+a)=(1+a)( ![]() +
+![]() a)=k.
a)=k.
解得:a1=1,a2=-2(舍去),∴k=![]() .
.
②当∠BAC=90°时,如图3,过点C作CM⊥x轴于点M,过点B作BN⊥x轴于点N,则∠CMA=∠CAB=∠ANB=90°,∴∠MCA+∠CAM=∠BAN+∠CAM=90°,∴∠MCA=∠BAN.由(1)知∠B=45°,∴△ABC是等腰直角三角形,∴AC=AB.
由①知△MAC∽△NBA,∴△MAC≌△NBA(AAS),∴AM=BN=![]() .
.
设CM=AN=b,则ON=3+b,∴B(3+b, ![]() ),C(3-
),C(3-![]() ,b).
,b).
∵点B,C在函数y=![]() (x>0)的图像上,∴
(x>0)的图像上,∴![]() (3+b)=(3-
(3+b)=(3-![]() )b=k,
)b=k,
解得:b=9![]() +12,∴k=18+15
+12,∴k=18+15![]() .
.
综上所述:k=4![]() 或18+15
或18+15![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
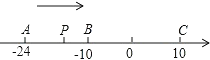
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA=________,PC=________;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:问题:![]() 能化为分数形式吗?
能化为分数形式吗?
探求:步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ,
,
步骤④![]() ,解得
,解得![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是____________;
(2)仿照上述探求过程,请你尝试把![]() 化为分数形式;
化为分数形式;
步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③__________________,
步骤④____________,解得![]() ____________;
____________;
(3)请你将![]() 化为分数形式,并说明理由。
化为分数形式,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:
问题:0.![]() 能用分数表示吗?
能用分数表示吗?
探求:步骤①设x=0.![]() ,
,
步骤②10x=10×0.![]() ,
,
步骤③10x=8.![]() ,
,
步骤④10x=8+0.![]() ,
,
步骤⑤10x=8+x,
步骤⑥9x=8,
步骤⑦x=![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是______;
(2)仿照上述探求过程,请你尝试把0.![]() 表示成分数的形式.
表示成分数的形式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED 灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了 LED 灯泡与普通白炽灯泡共 300 个,LED 灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利 3 200 元,求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120 个, 在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的 30%, 并求出此时这批灯泡的总利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天上午出租车司机小张在东西走向的大街上营运,如果规定向东为正,向西为负,他这天上午所接送六位乘客的行驶里程(单位:km)如下表:(等待乘客时,空车里程忽略不计)
乘客顺序 | 第一位 | 第二位 | 第三位 | 第四位 | 第五位 | 第六位 |
行驶里程 | -2 | +8 | -1 | +1 | -9 | -2 |
(1)将最后一位乘客送到目的地时,小张在出发地什么位置?
(2)若汽车耗油量为0.06![]() ,这天上午小张接送乘客,出租车共耗油多少升?
,这天上午小张接送乘客,出租车共耗油多少升?
(3)若出租车起步价为5元,起步里程为3km(包括3km),超过部分1.2元/km,问小张这天上午共收车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习概率知识后,小庆和小丽设计了一个游戏,在一个不透明的布袋A里面装有三个分别标有数字3,4,5的小球(小球除数字不同外,其余都相同);同时制作了一个可以自由转动的转盘B,转盘B被平均分成2部分,在每一部分内分别标上数字1,2.现在其中一人从布袋A中随机摸取一个小球,记下数字为x;另一人转动转盘B,转盘停止后,指针指向的数字记为y(若指针指在边界线上时视为无效,重新转动),从而确定点P的坐标为P(x,y).
(1)请用树状图或列表的方法写出所有可能得到的点P的坐标;
(2)若S=xy,当S为奇数时小庆获胜,否则小丽获胜,你认为这个游戏公平吗?对谁更有利呢?

查看答案和解析>>
科目:初中数学 来源: 题型:
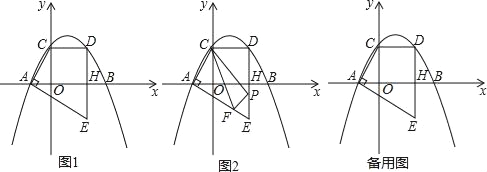
【题目】如图1,已知抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
(1)求线段DE的长度;
(2)如图2,试在线段AE上找一点F,在线段DE上找一点P,且点M为直线PF上方抛物线上的一点,求当△CPF的周长最小时,△MPF面积的最大值是多少;
(3)在(2)问的条件下,将得到的△CFP沿直线AE平移得到△C′F′P′,将△C′F′P′沿C′P′翻折得到△C′P′F″,记在平移过称中,直线F′P′与x轴交于点K,则是否存在这样的点K,使得△F′F″K为等腰三角形?若存在求出OK的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com