
【题目】如图1,已知抛物线y=﹣![]() x2+
x2+![]() x+
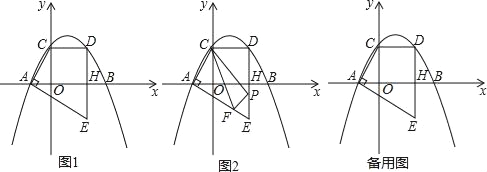
x+![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x轴于点H,过点A作AE⊥AC交DH的延长线于点E.
(1)求线段DE的长度;
(2)如图2,试在线段AE上找一点F,在线段DE上找一点P,且点M为直线PF上方抛物线上的一点,求当△CPF的周长最小时,△MPF面积的最大值是多少;
(3)在(2)问的条件下,将得到的△CFP沿直线AE平移得到△C′F′P′,将△C′F′P′沿C′P′翻折得到△C′P′F″,记在平移过称中,直线F′P′与x轴交于点K,则是否存在这样的点K,使得△F′F″K为等腰三角形?若存在求出OK的值;若不存在,说明理由.
【答案】(1)2![]() ;(2)
;(2) ![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)根据解析式求得C的坐标,进而求得D的坐标,即可求得DH的长度,令y=0,求得A,B的坐标,然后证得△ACO∽△EAH,根据对应边成比例求得EH的长,进继而求得DE的长;
(2)找点C关于DE的对称点N(4,![]() ),找点C关于AE的对称点G(-2,-
),找点C关于AE的对称点G(-2,-![]() ),连接GN,交AE于点F,交DE于点P,即G、F、P、N四点共线时,△CPF周长=CF+PF+CP=GF+PF+PN最小,根据点的坐标求得直线GN的解析式:y=
),连接GN,交AE于点F,交DE于点P,即G、F、P、N四点共线时,△CPF周长=CF+PF+CP=GF+PF+PN最小,根据点的坐标求得直线GN的解析式:y=![]() x-
x-![]() ;直线AE的解析式:y= -
;直线AE的解析式:y= -![]() x-
x-![]() ,过点M作y轴的平行线交FH于点Q,设点M(m,-
,过点M作y轴的平行线交FH于点Q,设点M(m,-![]() m+
m+![]() m+
m+![]() ),则Q(m,
),则Q(m,![]() m-
m-![]() ),根据S△MFP=S△MQF+S△MQP,得出S△MFP= -
),根据S△MFP=S△MQF+S△MQP,得出S△MFP= -![]() m+
m+![]() m+
m+![]() ,根据解析式即可求得,△MPF面积的最大值;
,根据解析式即可求得,△MPF面积的最大值;
(3)由(2)可知C(0,![]() ),F(0,
),F(0,![]() ),P(2,
),P(2,![]() ),求得CF=
),求得CF=![]() ,CP=
,CP=![]() ,进而得出△CFP为等边三角形,边长为
,进而得出△CFP为等边三角形,边长为![]() ,翻折之后形成边长为
,翻折之后形成边长为![]() 的菱形C′F′P′F″,且F′F″=4,然后分三种情况讨论求得即可.
的菱形C′F′P′F″,且F′F″=4,然后分三种情况讨论求得即可.
本题解析:(1)对于抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() ,
,
令x=0,得y=![]() ,即C(0,
,即C(0,![]() ),D(2,
),D(2,![]() ),
),
∴DH=![]() ,
,
令y=0,即﹣![]() x2+
x2+![]() x+
x+![]() =0,得x1=﹣1,x2=3,
=0,得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
∵AE⊥AC,EH⊥AH,
∴△ACO∽△EAH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:EH=![]() ,
,
则DE=2![]() ;
;
(2)找点C关于DE的对称点N(4,![]() ),找点C关于AE的对称点G(﹣2,﹣
),找点C关于AE的对称点G(﹣2,﹣![]() ),
),
连接GN,交AE于点F,交DE于点P,即G、F、P、N四点共线时,△CPF周长=CF+PF+CP=GF+PF+PN最小,
直线GN的解析式:y=![]() x﹣
x﹣![]() ;直线AE的解析式:y=﹣
;直线AE的解析式:y=﹣![]() x﹣
x﹣![]() ,
,
联立得:F (0,﹣![]() ),P(2,
),P(2,![]() ),
),
过点M作y轴的平行线交FH于点Q,
设点M(m,﹣![]() m2+
m2+![]() m+
m+![]() ),则Q(m,
),则Q(m,![]() m﹣
m﹣![]() ),(0<m<2);
),(0<m<2);
∴S△MFP=S△MQF+S△MQP=![]() MQ×2=MQ=﹣
MQ×2=MQ=﹣![]() m2+
m2+![]() m+
m+![]()
![]() ,
,
∵对称轴为:直线m=![]() <2,开口向下,
<2,开口向下,
∴m=![]() 时,△MPF面积有最大值:
时,△MPF面积有最大值:![]()
![]() ;
;
(3)由(2)可知C(0,![]() ),F(0,
),F(0,![]() ),P(2,
),P(2,![]() ),
),
∴CF=![]() ,CP=
,CP=![]() =
=![]() ,
,
∵OC=![]() ,OA=1,
,OA=1,
∴∠OCA=30°,
∵FC=FG,
∴∠OCA=∠FGA=30°,
∴∠CFP=60°,
∴△CFP为等边三角形,边长为![]() ,
,
翻折之后形成边长为![]() 的菱形C′F′P′F″,且F′F″=4,
的菱形C′F′P′F″,且F′F″=4,
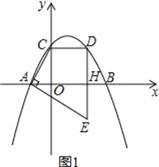
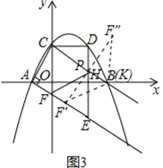
1)当K F′=KF″时,如图3,
点K在F′F″的垂直平分线上,所以K与B重合,坐标为(3,0),
∴OK=3;
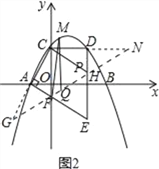
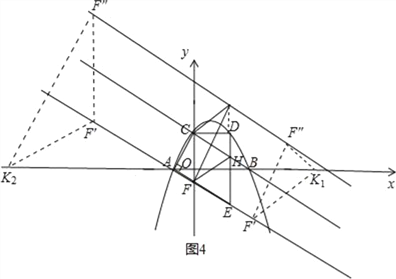
2)当F′F″=F′K时,如图4,
∴F′F″=F′K=4,
∵FP的解析式为:y=![]() x﹣
x﹣![]() ,
,
∴在平移过程中,F′K与x轴的夹角为30°,
∵∠OAF=30°,
∴F′K=F′A
∴AK=4![]()
∴OK=4![]() ﹣1或者4
﹣1或者4![]() +1;
+1;
3)当F″F′=F″K时,如图5,
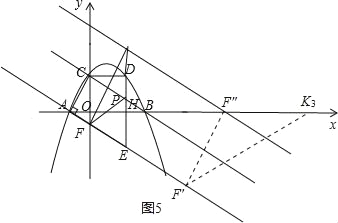
∵在平移过程中,F″F′始终与x轴夹角为60°,
∵∠OAF=30°,
∴∠AF′F″=90°,
∵F″F′=F″K=4,
∴AF″=8,
∴AK=12,
∴OK=11,
综上所述:OK=3,4![]() ﹣1,4
﹣1,4![]() +1或者11.
+1或者11.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为 ;
(2)如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;
(3)如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y=![]() (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为
(x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为![]() .当△ABC是直角三角形时,求 k 的值.
.当△ABC是直角三角形时,求 k 的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
(1)稿费不高于800元的不纳税;
(2)稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
(3)稿费为4000元或高于4000元的应缴纳全部稿费的11%的税,
试根据上述纳税的计算方法作答:
①若王老师获得的稿费为2400元,则应纳税________元,若王老师获得的稿费为4000元,则应纳税________元.
②若王老师获稿费后纳税420元,求这笔稿费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
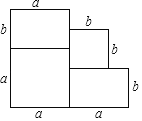
【题目】如图是一所住宅的建筑平面图.
(1)用含有a、b的式子表示这所住宅的建筑面积.
(2)当a=5米,b=4米时,住宅的建筑面积有多大?
(3)在(2)的条件下,若此住宅的销售单价为每平方米5000元,求此住宅的销售价是多少元?(结果用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2019=( )
A.(31,47)B.(31,48)C.(32,48)D.(32,49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 25 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=30°,点D在△ABC外,且BD=2.连AD、CD,则△ACD的周长最小值为( )

A. 1B. ![]() C. 2D. 2
C. 2D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com