【题目】如图，矩形
中，
，
，
是
边上一点，将
沿
翻折，点
恰好落在对角线
上的点
处，则
的长为________．
【答案】3
【解析】
利用矩形的性质得到BC=AD=8，∠ABC=90°，再根据勾股定理计算出AC=10，接着利用折叠的性质得∠AFE=∠ABE=90°，AF=AB=6，BE=FE，所以CF=4，设BE=x，则EF=x，CE=8-x，利用勾股定理得到x2+42=（8-x）2，解得x=3，即可得出结论.
∵四边形ABCD为矩形，
∴BC=AD=8，∠ABC=90°，
在Rt△ABC中，AC=
，
∵△ABE沿AE翻折，点B恰好落在对角线AC上的点F处，
∴∠AFE=∠ABE=90°，AF=AB=6，BE=FE，
∴CF=10-6=4，
设BE=x，则EF=x，CE=8-x，
在Rt△CEF中，x2+42=（8-x）2，解得x=3，
∴BE=3，
故答案为：3.
智能训练练测考系列答案科目：初中数学 来源： 题型：
【题目】济宁市全运会会期间，邹城市投资150万元引进一项大型游乐设施．若不计维修保养费用，预计开放后每月可创收33万元．而该游乐设施开放后，从第1个月到第x个月的维修保养费用累计为y（万元），且y=ax2+ bx；若将创收扣除投资和维修保养费用 称为游乐场的纯收益g（万元），g也是关于 x的二次函数；
（1）若维修保养费用第1个月为2万元，第2个月为4万元．求y关于x的解析式；
（2）求纯收益g关于x的解析式；
（3）问设施开放几个月后，游乐场的纯收益达到最大；几个月后，能收回投资？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，己知线段AB=20cm，CD=2cm，线段
在线段
上运动，
分别是AC，BC的中点.
(1)若
=4cm，则
=______cm.
(2)当线段在线段上运动时，试判断的长度是否发生变化?如果不变请求出的长度，如果变化，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一边是另一边的
倍的三角形叫做智慧三角形，这两边中较长边称为智慧边，这两边的 夹角叫做智慧角．
（1）在 Rt△ABC 中，∠ACB＝90°，若∠A 为智慧角，则∠B 的度数为 ；
（2）如图①，在△ABC 中，∠A＝45°，∠B＝30°，求证：△ABC 是智慧三角形；
（3）如图②，△ABC 是智慧三角形，BC 为智慧边，∠B 为智慧角，A（3，0），点 B，C 在函数 y＝
（x＞0）的图像上，点 C 在点 B 的上方，且点 B 的纵坐标为
．当△ABC是直角三角形时，求 k 的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料，回答下列问题：
数轴是学习有理数的一种重要工具，任何有理数都可以用数轴上的点表示，这样能够运用数形结合的方法解决一些问题。例如，两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示；
在数轴上，有理数3与1对应的两点之间的距离为|31|=2；
在数轴上,有理数5与2对应的两点之间的距离为|5(2)|=7；
在数轴上，有理数2与3对应的两点之间的距离为|23|=5；
在数轴上,有理数8与5对应的两点之间的距离为|8(5)|=3；……
如图1，在数轴上有理数a对应的点为点A，有理数b对应的点为点B，A，B两点之间的距离表示为|ab|或|ba|，记为|AB|=|ab|=|ba|.
(1)数轴上有理数10与5对应的两点之间的距离等于___；数轴上有理数x与5对应的两点之间的距离用含x的式子表示为___；若数轴上有理数x与1对应的两点A，B之间的距离|AB|=2，则x等于___；
(2)如图2，点M，N，P是数轴上的三点，点M表示的数为4，点N表示的数为2，动点P表示的数为x.
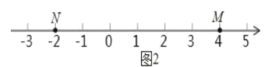
①若点P在点M，N之间，则|x+2|+|x4|=___；若|x+2|+|x4|═10，则x=___；
②根据阅读材料及上述各题的解答方法，|x+2|+|x|+|x2|+|x4|的最小值等于___.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图．在△ABC中，BA=BC，以AB为直径的⊙O分别交AC，BC于点D、E，BC的延长线与⊙O的切线AF交于点F．
（1）求证：∠ABC=2∠CAF；
（2）已知AC=2
，EB=4CE，求⊙O的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲地的海拔高度是
米，乙地的海拔高度比甲地海拔高度的
倍多
米，丙地的海拔高度比甲地海拔高度的
倍少
米．
(1) 三地的海拔高度和一共是多少米？；
(2) 乙地的海拔高度比丙地的海拔高度高多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】华联超市第一次用7000元购进甲、乙两种商品，其中甲商品的件数是乙商品件数的2倍，甲、乙两种商品的进价和售价如表：(注：获利＝售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 25 | 40 |
(1)该超市购进甲、乙两种商品各多少件？
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
(3)该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍：甲商品按原价销售，乙商品打折销售，第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元，求第二次乙商品是按原价打几折销售？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com