
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)a<1或a>3
;(3)a<1或a>3
【解析】
(1)抛物线C:y=ax2-2ax+3与y轴交于点A,令x=0,即可求得A的坐标;
(2)令y=0,解方程即可求得B的坐标,然后根据待定系数法即可求得直线l的解析式;
(3)当a=3时,抛物线C过点B(1,0),此时k=-3.当a=-1时,抛物线C过点B(3,0),此时k=-1.结合图象即可求得.
(1)∵抛物线C:y=ax22ax+3与y轴交于点A,
∴点A的坐标为(0,3).
(2)当a=1时,抛物线C为y=x2+2x+3.
∵抛物线C与x轴交于点B,且点B在x轴的正半轴上,
∴点B的坐标为(3,0).
∵直线l:y=kx+b过A,B两点,
∴![]() .解得
.解得![]() .
.
∴直线l的解析式为y=x+3.
(3)如图,
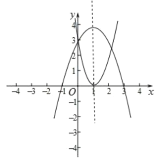
当a>0时,
当a=3时,抛物线C过点B(1,0),此时k=3.
结合函数图象可得a>3.
当a<0时,
当a=1时,抛物线C过点B(3,0),此时k=1.
结合函数图象可得a<1.
综上所述,a的取值范围是a<1或a>3.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ;
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
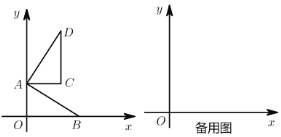
【题目】如图,在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,且
,且![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得
,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .
.
(1)点![]() 的坐标为______.
的坐标为______.
(2)解答下列问题:
①设![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
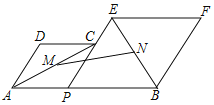
【题目】如图,已知AB=12,P为线段AB上的一个动点,分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE,点P、C、E在一条直线上,∠DAP=60°.M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为______.(结果留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种商品,每件成本为30元.经市场调研,售价为40元时,每月可销售200件;售价每涨1元,每月销售量将减少10件.该商场每月要在这种商品上盈利2160元的同时.尽可能的减少库存,那么这种商品售价应该定为多少元?
(1)解:方法1:设这种商品的定价为![]() 元,由题意,得方程为: ;
元,由题意,得方程为: ;
方法2:设这种商品涨了![]() 元,由题意,得方程为: ;
元,由题意,得方程为: ;
(2)请你选择一种方法,写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
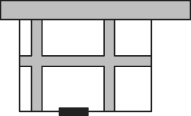
【题目】某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米.
(1)为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光下,小东同学测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.
米.

![]() 同一时刻
同一时刻![]() 米的竹竿的影长为________米.
米的竹竿的影长为________米.
![]() 同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,测得落在第一级台阶上的影子长为
同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,测得落在第一级台阶上的影子长为![]() 米,第一级台阶的高为
米,第一级台阶的高为![]() 米,落在地面上的影子长为
米,落在地面上的影子长为![]() 米,则树的高度为________米.
米,则树的高度为________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com