
【题目】如图,在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,且
,且![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得
,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .
.
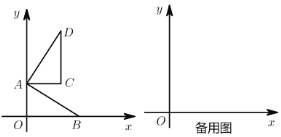
(1)点![]() 的坐标为______.
的坐标为______.
(2)解答下列问题:
①设![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ,或
,或![]() ,
,![]() .②
.②![]() ,
,![]() 或
或![]() .
.
【解析】
(1)由旋转的性质得出AC=AO=8,∠OAC=90°,得出C(8,8)即可;(2)①由旋转的性质得出DC=OB=m,∠ACD=∠AOB=90°,∠OAC=90°,得出∠ACE=90°,证出四边形OACE是矩形,得出DE⊥x主,OE=AC=8,分三种情况:a、当点B在线段OE的延长线上时,得出BE=OB-OE=m-8,由三角形的面积公式得出S=![]() m2-4m(m>8)即可; b、当点B在线段OE上(点B不与O,E重合)时,BE=OE-OB=8-m,由三角形的面积公式得出S=-
m2-4m(m>8)即可; b、当点B在线段OE上(点B不与O,E重合)时,BE=OE-OB=8-m,由三角形的面积公式得出S=-![]() m2+4m(0<m<8)即可;c、当点B与E重合时,即m=8,△BCD不存在;
m2+4m(0<m<8)即可;c、当点B与E重合时,即m=8,△BCD不存在;
②当S=6,m>8时,得出![]() m2-4m=6,解方程求出m即可;当S=6,0<m<8时,得出-
m2-4m=6,解方程求出m即可;当S=6,0<m<8时,得出-![]() m2+4m=6,解方程求出m即可.
m2+4m=6,解方程求出m即可.
解:(1)∵点A(0,8),
∴AO=8,
∵△AOB绕点A逆时针旋转90°得△ACD,
∴AC=AO=8,∠OAC=90°,
∴C(8,8),
故答案为:(8,8);
(2)①延长DC交x轴于点E,
∵点B(m,0),
∴OB=m,
∵△AOB绕点A逆时针旋转90°得△ACD,
∴DC=OB=m,∠ACD=∠AOB=90°,∠OAC=90°,
∴∠ACE=90°,
∴四边形OACE是矩形,
∴DE⊥x主,OE=AC=8,
分三种情况:
a、当点B在线段OE的延长线上时,如图1所示:
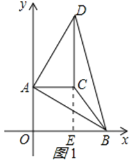
则BE=OB-OE=m-8,
∴S=![]() DCBE=
DCBE=![]() m(m-8),
m(m-8),
即S=![]() m2-4m(m>8);
m2-4m(m>8);
b、当点B在线段OE上(点B不与O,E重合)时,如图2所示:
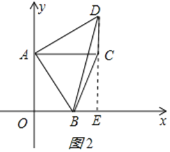
则BE=OE-OB=8-m,
∴S=![]() DCBE=
DCBE=![]() m(8-m),
m(8-m),
即S=-![]() m2+4m(0<m<8);
m2+4m(0<m<8);
c、当点B与E重合时,即m=8,△BCD不存在;
综上所述,S=![]() m2-4m(m>8),或S=-
m2-4m(m>8),或S=-![]() m2+4m(0<m<8);
m2+4m(0<m<8);
②当S=6,m>8时,![]() m2-4m=6,
m2-4m=6,
解得:m=4±2![]() (负值舍去),
(负值舍去),
∴m=4+2![]() ;
;
当S=6,0<m<8时,-![]() m2+4m=6,
m2+4m=6,
解得:m=2或m=6,
∴点B的坐标为(4+2![]() ,0)或(2,0)或(6,0).
,0)或(2,0)或(6,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,下列结论:①抛物线过点
,其部分图象如图所示,下列结论:①抛物线过点![]() ;②
;②![]() ;③
;③![]() ;④抛物线的顶点坐标为
;④抛物线的顶点坐标为![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 增大而增大.其中结论错误的是( )
增大而增大.其中结论错误的是( )
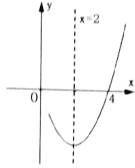
A.②③④B.②③⑤C.③⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )

A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表:方程1、方程2、方程3、…是按一定规律排列的一列方程.
序号 | 方程 | 方程的解 | |
1 | x2+x﹣2﹣=0 | x1=﹣2 | x2=1 |
2 | x2+2x﹣8﹣=0 | x1=﹣4 | x2=2 |
3 | x2+3x﹣18=0 | x1= | x2= |
… | … | … | … |
(1)解方程3,并将它的解填在表中的空白处;
(2)请写出这列方程中第10个方程,并用求根公式求其解.
(3)根据表中的规律写出第n个方程和这个方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,
,
下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④若点![]() ,点
,点![]() ,点
,点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;
⑤若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .
.
其中正确的结论有( )
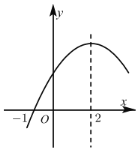
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
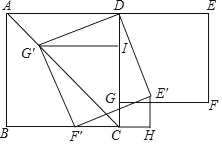
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网购已经成为一种时尚,某网络购物平台“双十一”全天交易额逐年增长,2016年交易额为500亿元,2018年交易额为720亿元。
(1)2016年至2018年“双十一”交易额的年平均增长率是多少?
(2)若保持原来的增长率,试计算2019年该平台“双十一”的交易额将达到多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com