
【题目】用合适的方法解方程:
(1)(2t+3)2=3(2t+3)
(2)(2x﹣1)2=9(x﹣2)2
(3)2x2=5x﹣1
(4)x2+4x﹣5=0
【答案】(1)t1=﹣![]() ,t2=0;(2)x1=
,t2=0;(2)x1=![]() ,x2=5;(3)
,x2=5;(3)![]() ;(4)x1=1,x2=﹣5
;(4)x1=1,x2=﹣5
【解析】
(1)等号的左右两边都有(2t+3),可移项然后用因式分解法解此方程.
(2)等号的左右两边都有平方,可移项然后用因式分解法解此方程.
(3)此题可采用公式法解,先化成一般形式,代入公式即可.
(4)此题可采用十字相乘法或者是配方法即可.
(1)(2t+3)2=3(2t+3)
(2t+3)2﹣3(2t+3)=0
(2t+3)(2t+3﹣3)=0
∴2t+3=0或2t=0
∴t1=﹣![]() ,t2=0.
,t2=0.
(2)(2x﹣1)2=9(x﹣2)2
(2x﹣1)2﹣9(x﹣2)2=0
(2x﹣1+3x﹣6)(2x﹣1﹣3x+6)=0
5x﹣7=0或﹣x+5=0
∴x1=![]() ,x2=5.
,x2=5.
(3)2x2=5x﹣1
2x2﹣5x+1=0
x=![]()
∴x1=![]() ,x2=
,x2=![]() .
.
(4)x2+4x﹣5=0
(x﹣1)(x+5)=0
x1=1,x2=﹣5.
或者x2+4x+4=9
(x+2)2=±3
∴x+2=3或x+2=﹣3
∴x1=1,x2=﹣5.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,且
,且![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得
,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .
.
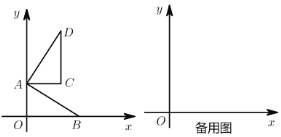
(1)点![]() 的坐标为______.
的坐标为______.
(2)解答下列问题:
①设![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种商品,每件成本为30元.经市场调研,售价为40元时,每月可销售200件;售价每涨1元,每月销售量将减少10件.该商场每月要在这种商品上盈利2160元的同时.尽可能的减少库存,那么这种商品售价应该定为多少元?
(1)解:方法1:设这种商品的定价为![]() 元,由题意,得方程为: ;
元,由题意,得方程为: ;
方法2:设这种商品涨了![]() 元,由题意,得方程为: ;
元,由题意,得方程为: ;
(2)请你选择一种方法,写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
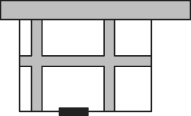
【题目】某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米.
(1)为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光下,小东同学测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.
米.

![]() 同一时刻
同一时刻![]() 米的竹竿的影长为________米.
米的竹竿的影长为________米.
![]() 同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,测得落在第一级台阶上的影子长为
同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,测得落在第一级台阶上的影子长为![]() 米,第一级台阶的高为
米,第一级台阶的高为![]() 米,落在地面上的影子长为
米,落在地面上的影子长为![]() 米,则树的高度为________米.
米,则树的高度为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
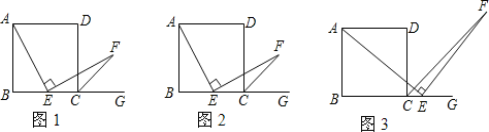
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:在AB上截取BM=BE,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立。你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com