
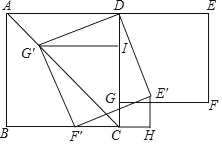
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】试题解析:作G′I⊥CD于I,G′R⊥BC于R,E′H⊥BC交BC的延长线于H.连接RF′.则四边形RCIG′是正方形.
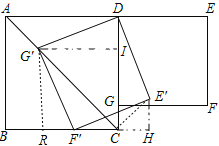
∵∠DG′F′=∠IGR=90°,∴∠DG′I=∠RG′F′,在△G′ID和△G′RF中,∵G′D= G′F,∠D G′I=∠R G′F′,G′I= G′R,∴△G′ID≌△G′RF,∴∠G′ID=∠G′RF′=90°,∴点F′在线段BC上,在Rt△E′F′H中,∵E′F′=2,∠E′F′H=30°,∴E′H=![]() E′F′=1,F′H=
E′F′=1,F′H=![]() ,易证△RG′F′≌△HF′E′,∴RF′=E′H,RG′RC=F′H,∴CH=RF′=E′H,∴CE′=
,易证△RG′F′≌△HF′E′,∴RF′=E′H,RG′RC=F′H,∴CH=RF′=E′H,∴CE′=![]() ,∵RG′=HF′=
,∵RG′=HF′=![]() ,∴CG′=
,∴CG′=![]() RG′=
RG′=![]() ,∴CE′+CG′=
,∴CE′+CG′=![]() .
.
故选A.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
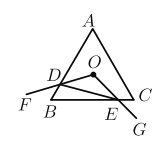
【题目】如图,等边三角形ABC的边长为4, 点O是![]() 的中心, ∠FOG = 120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、 E两点,连接DE,给出下列四个结论:①OD= OE;②
的中心, ∠FOG = 120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、 E两点,连接DE,给出下列四个结论:①OD= OE;②![]() ;③四边形ODBE的面积始终等于
;③四边形ODBE的面积始终等于![]() ;④
;④![]() 周长的最小值为6.上述结论中正确的有_________(写出序号)
周长的最小值为6.上述结论中正确的有_________(写出序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
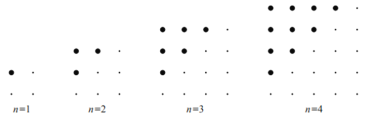
【题目】在下图中,每个正方形点阵由大点和小点组成:
(1)第7个正方形点阵中,大点和小点的总共的个数是________其中大点的个数是_________.
(2)第n个图形中,大点的个数是__________;(用含n的式子表示)
(3)是否存在某个图形,使得大点的个数是210个?若存在,请求出n的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
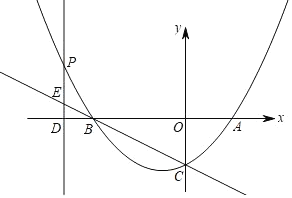
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,且
,且![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得
,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .
.
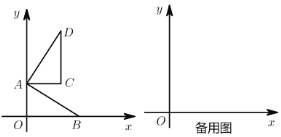
(1)点![]() 的坐标为______.
的坐标为______.
(2)解答下列问题:
①设![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,其他三边用总长为60米栅栏围住(如图),若设绿化带的BC边为x米,绿化带的面积为y平方米。

(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围:
(2)是否存在绿化带BC的长的某个值,使得绿化带的面积为450平方米?若存在,请求出这个值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com